5.8 KiB

Raw Blame History

Solution Overview

In the solution explained below, we enable a peer to to perform the operations described in Formal Problem Definition by only holding O(logn) many tree nodes (but not the entire tree).

The solution relies on the following statement:

In a Merkle Tree with the capacity of n leaves , one can compute the root of the tree by maintaining the root nodes of log(n) number of complete Merkle trees.

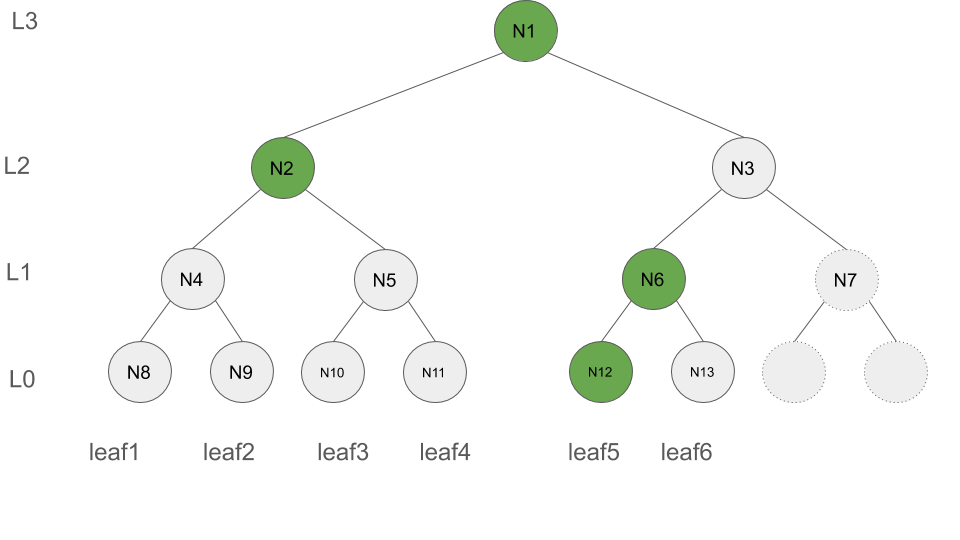
We use the preciding observation and define F = [(L:0, H0, leafIndex0), ..., (L:d, Hd, leafIndexd)] to be an array of size log(n)+1 holding the root of the complete Merkle trees (all positioned on the left side of the tree) for levels [0, ..., d=log(n)]. Each entry of F is a tuple (L, leafIndex, H) in which His the root of the complete subtree at level L, and leafIndex indicates the index of the leaf node whose insertion resulted in H. The storage of leafIndex in each tuple will later enables the efficient support of deletion operation. Each peer shall store F locally.

For the Merkle Tree shown in Figure below, F = [(L:0, N12, leafIndex:5), (L:1, N6, leafIndex:6), (L:2, N2, leafIndex:4), (L:3, N1, leafIndex:6)] is highlighted in green. Note that F only contains the green nodes but none of the gray nodes.

Computing the root after deletion

Given that F is stored by each peer locally, we demonestrate how deletion can be supported relying on F.

When a node gets deleted, its authentication path is available, and the following solution relies on that.

Consider the deletion of the leafIndex:i with the authentication path / (membership proof) of the follwoing form authpath = [(L:0, H0), ..., (L:d, Hd)] where in each tuple H represents the value of the merkle tree node along the authentication path of leaf i at the corresponding level L. Note that d varies from 0 to logn. The last entry of authpath i.e., (L:d, Hd) is indeed the tree root.

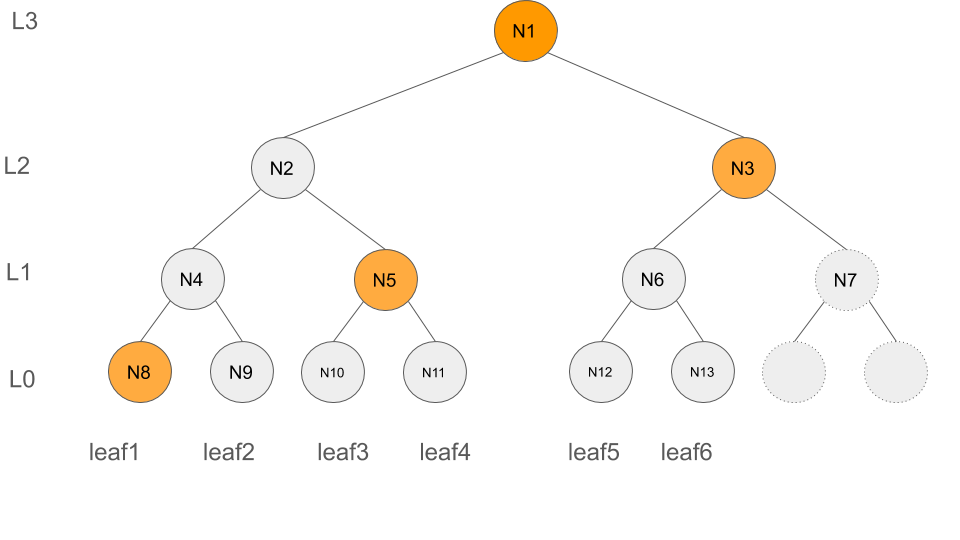
The authentication path of leafIndex:2 is illustrated in the following figure (highlighted in yellow) and consists of authpath2 = [(L:0, N8), (L:1, N5), (L:2, N3), (L:3, N1)].

We need to update F based on authpath2. In specific, we need to determine whether any of the nodes whose values get altered as the result of deletion of a leaf node intersect with the nodes in F, and if this is the case the corresponding nodes in F shall get updated too.

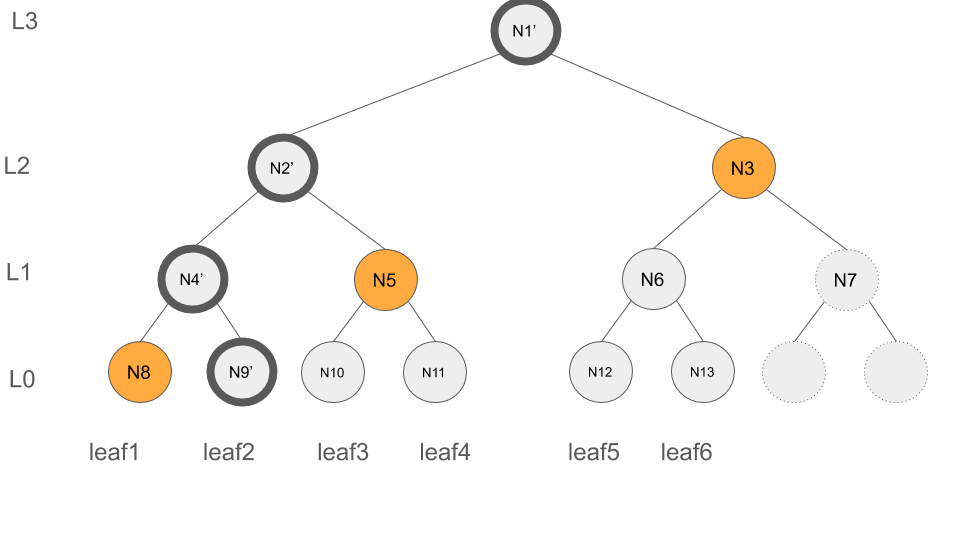
Lets clarify it by the help of an example. Consider leafIndex:2, the deletion of leafIndex:2 impacts N9 (level 0), N4 (level 1), N2 (level 2) and N1 (level 3)(root) of the tree, as illustrated below with the dark circles.

Thus, in order to update F, we need to update those entries of F that contain N9, N4, N2 or N1.

To do so, we determine whether for each tuple (L, leafIndex, H) in F, the leafIndex and the deleted leaf node have the same ancestor at level L. We use HasCommAnc method to perform this check, it is later defined in Common ancestor subsection. For example, leaf2 and leaf4 have the same ancestor at level 2, which is N2, thus HasCommAnc(2,4,2) return true.

Following our previous example, in order to find out whether N9, N4, N2 or N1 belong to F we proceed as follows.

inputs:
- Index of the deleted node leafIndex:2
- F = [(L:0, N12, leafIndex:5), (L:1, N6, leafIndex:6), (L:2, N2, leafIndex:4), (L:3, N1, leafIndex:6)]
Update procedure of F:
- level L:0, HasCommAnc(leafIndex:2, leafIndex:5, L:0) = false, thus F does not change
- level L:1, HasCommAnc(leafIndex:2, leafIndex:6, L:1) = false, thus F does not change
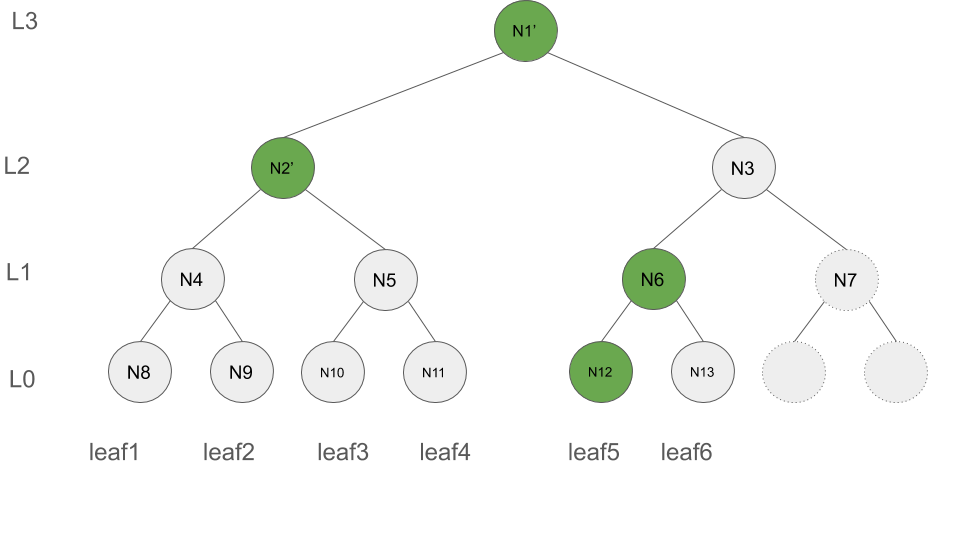
- level L:2, HasCommAnc(leafIndex:2, leafIndex:4, L:2) = true, thus F = [(L:0, N12, leafIndex:5), (L:1, N6, leafIndex:6), (L:2, N2', leafIndex:4), (L:3, N1, leafIndex:6)]
- level L:3, HasCommAnc(leafIndex:2, leafIndex:6, L:3) = true, thus F = [(L:0, N12, leafIndex:5), (L:1, N6, leafIndex:6), (L:2, N2', leafIndex:4), (L:3, N1', leafIndex:6)]
Output
- F' = [(L:0, N12, leafIndex:5), (L:1, N6, leafIndex:6), (L:2, N2', leafIndex:4), (L:3, N1', leafIndex:6)]

Common Ancestor

In order to determine whether two nodes with indices i and j have common anscestor at a particular level lev, the followong formula can be applied

check whether floor( (i-1)/2^lev ) is equal to floor( (j-1)/2^lev )

Update tree root after deletion

Inputs (the levels i.e., L values are removed since the position of each entry can represent its level):
- F = [(H0,index0), ..., (Hd,indexd)]
- leafIndex ( The index of the deleted leaf)
- authpath = [H0, ..., Hd] (The authentication path of the deleted leaf)
- Z = [H(0), H(Z[0]||Z[0]), H(Z[1]||Z[1]), ..., H(Z[d-1]||Z[d-1])]
Output: F which is the updated F

path = binary representation of leafIndex - 1
acc = Z[0]
for lev in 0..d # d inclusive
  if HasCommAnc(leafIndex, F[lev].index,lev) == true # F[lev].index has common ancestor with leafIndex at level lev 
    F[l] = acc
  if the last bit of path is 1
    acc = H(authPath[lev], acc)
  else
    acc = H(acc, authPath[lev])
  shift path right by 1

HasCommAnc(i, j, lev) =
  return floor( (i-1)/2^lev ) == floor( (j-1)/2^lev )

Updating authentication paths

Lets index the tree nodes following the formula below, for each tree node with index i, its right and left child have index 2*i and 2*i+1, respectively. The root has index 1. The sample tree is illustrated below.

When a node gets deleted,

While writing up the preceding solution, I came up with a simiplified version in which we do not need to store the the leaf indices, instead we can compute them on the fly.

5.8 KiB Raw Blame History