mirror of
https://github.com/status-im/secp256k1.git
synced 2025-02-24 11:48:18 +00:00
d2f9c6b Use more precise pippenger bucket windows (Jonas Nick) 4c950bb Save some additions per window in _pippenger_wnaf (Peter Dettman) a58f543 Add flags for choosing algorithm in ecmult_multi benchmark (Jonas Nick) 36b22c9 Use scratch space dependent batching in ecmult_multi (Jonas Nick) 355a38f Add pippenger_wnaf ecmult_multi (Jonas Nick) bc65aa7 Add bench_ecmult (Pieter Wuille) dba5471 Add ecmult_multi tests (Andrew Poelstra) 8c1c831 Generalize Strauss to support multiple points (Pieter Wuille) 548de42 add resizeable scratch space API (Andrew Poelstra) Pull request description: This PR is based on #473 and adds a variant of "Pippengers algorithm" (see [Bernstein et al., Faster batch forgery identification](https://eprint.iacr.org/2012/549.pdf), page 15 and https://github.com/scipr-lab/libff/pull/10) for point multi-multiplication that performs better with a large number of points than Strauss' algorithm. 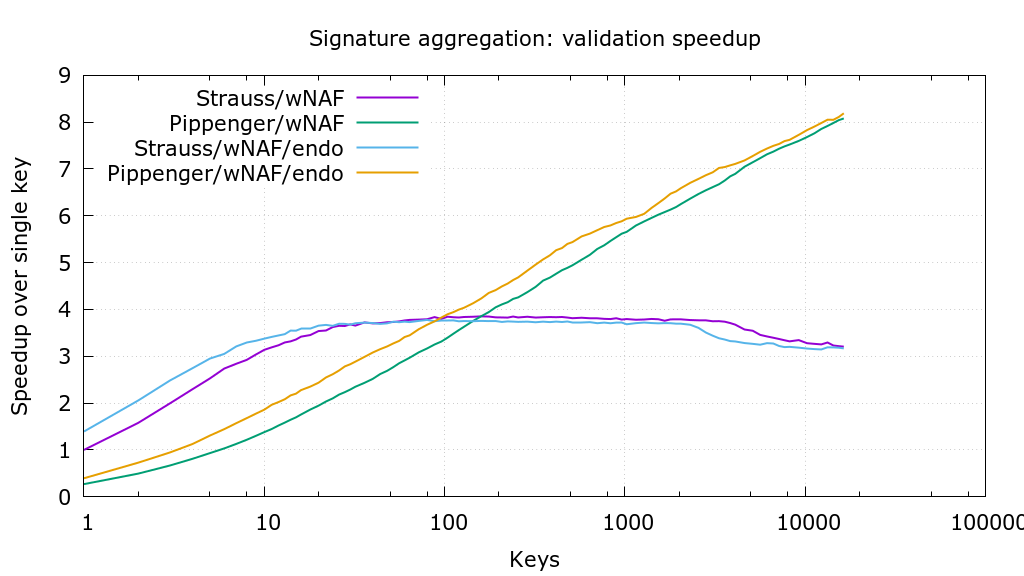 Thanks to @sipa for providing `wnaf_fixed`, benchmarking, and the crucial suggestion to use affine addition. The PR also makes `ecmult_multi` decide which algorithm to use, based on the number of points and the available scratch space. For restricted scratch spaces this can be further optimized in the future (f.e. a 35kB scratch space allows batches of 11 points with strauss or 95 points with pippenger; choosing pippenger would be 5% faster). As soon as this PR has received some feedback I'll repeat the benchmarks to determine the optimal `pippenger_bucket_window` with the new benchmarking code in #473. Tree-SHA512: 8e155107a00d35f412300275803f912b1d228b7adff578bc4754c5b29641100b51b9d37f989316b636f7144e6b199febe7de302a44f498bbfd8d463bdbe31a5c
libsecp256k1
Optimized C library for EC operations on curve secp256k1.
This library is a work in progress and is being used to research best practices. Use at your own risk.
Features:
- secp256k1 ECDSA signing/verification and key generation.
- Adding/multiplying private/public keys.
- Serialization/parsing of private keys, public keys, signatures.
- Constant time, constant memory access signing and pubkey generation.
- Derandomized DSA (via RFC6979 or with a caller provided function.)
- Very efficient implementation.
Implementation details
- General
- No runtime heap allocation.
- Extensive testing infrastructure.
- Structured to facilitate review and analysis.
- Intended to be portable to any system with a C89 compiler and uint64_t support.
- Expose only higher level interfaces to minimize the API surface and improve application security. ("Be difficult to use insecurely.")
- Field operations
- Optimized implementation of arithmetic modulo the curve's field size (2^256 - 0x1000003D1).
- Using 5 52-bit limbs (including hand-optimized assembly for x86_64, by Diederik Huys).
- Using 10 26-bit limbs.
- Field inverses and square roots using a sliding window over blocks of 1s (by Peter Dettman).
- Optimized implementation of arithmetic modulo the curve's field size (2^256 - 0x1000003D1).
- Scalar operations
- Optimized implementation without data-dependent branches of arithmetic modulo the curve's order.
- Using 4 64-bit limbs (relying on __int128 support in the compiler).
- Using 8 32-bit limbs.
- Optimized implementation without data-dependent branches of arithmetic modulo the curve's order.
- Group operations
- Point addition formula specifically simplified for the curve equation (y^2 = x^3 + 7).
- Use addition between points in Jacobian and affine coordinates where possible.
- Use a unified addition/doubling formula where necessary to avoid data-dependent branches.
- Point/x comparison without a field inversion by comparison in the Jacobian coordinate space.
- Point multiplication for verification (aP + bG).
- Use wNAF notation for point multiplicands.
- Use a much larger window for multiples of G, using precomputed multiples.
- Use Shamir's trick to do the multiplication with the public key and the generator simultaneously.
- Optionally (off by default) use secp256k1's efficiently-computable endomorphism to split the P multiplicand into 2 half-sized ones.
- Point multiplication for signing
- Use a precomputed table of multiples of powers of 16 multiplied with the generator, so general multiplication becomes a series of additions.
- Access the table with branch-free conditional moves so memory access is uniform.
- No data-dependent branches
- The precomputed tables add and eventually subtract points for which no known scalar (private key) is known, preventing even an attacker with control over the private key used to control the data internally.
Build steps
libsecp256k1 is built using autotools:
$ ./autogen.sh
$ ./configure
$ make
$ ./tests
$ sudo make install # optional
Description
Languages
C
91.7%
Sage
2.7%
Assembly
1.8%
CMake
1.4%
M4
1.3%
Other
1.1%