Cleaning up papers
|
Before Width: | Height: | Size: 14 KiB After Width: | Height: | Size: 14 KiB |
|
Before Width: | Height: | Size: 20 KiB After Width: | Height: | Size: 20 KiB |
|
Before Width: | Height: | Size: 27 KiB After Width: | Height: | Size: 27 KiB |
|
Before Width: | Height: | Size: 28 KiB After Width: | Height: | Size: 28 KiB |
|
|
@ -1,3 +0,0 @@
|
|||
discouragement.aux
|
||||
discouragement.log
|
||||
x.log
|
||||
|
Before Width: | Height: | Size: 16 KiB |
|
|
@ -1,11 +0,0 @@
|
|||
\relax
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {1}Principles}{1}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {2}Introduction, Protocol I}{2}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {3}Proof Sketch of Safety and Plausible Liveness}{4}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {4}Fork Choice Rule}{6}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {5}Dynamic Validator Sets}{7}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {6}Mass Crash Failure Recovery}{9}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {7}Conclusions}{10}}
|
||||
\bibstyle{abbrv}
|
||||
\bibdata{main}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {8}References}{11}}
|
||||
|
|
@ -1,260 +0,0 @@
|
|||
This is pdfTeX, Version 3.14159265-2.6-1.40.16 (TeX Live 2015/Debian) (preloaded format=pdflatex 2017.6.27) 20 AUG 2017 04:48
|
||||
entering extended mode
|
||||
restricted \write18 enabled.
|
||||
%&-line parsing enabled.
|
||||
**casper_basic_structure.tex
|
||||
(./casper_basic_structure.tex
|
||||
LaTeX2e <2016/02/01>
|
||||
Babel <3.9q> and hyphenation patterns for 3 language(s) loaded.
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
|
||||
Document Class: article 2014/09/29 v1.4h Standard LaTeX document class
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo
|
||||
File: size12.clo 2014/09/29 v1.4h Standard LaTeX file (size option)
|
||||
)
|
||||
\c@part=\count79
|
||||
\c@section=\count80
|
||||
\c@subsection=\count81
|
||||
\c@subsubsection=\count82
|
||||
\c@paragraph=\count83
|
||||
\c@subparagraph=\count84
|
||||
\c@figure=\count85
|
||||
\c@table=\count86
|
||||
\abovecaptionskip=\skip41
|
||||
\belowcaptionskip=\skip42
|
||||
\bibindent=\dimen102
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
|
||||
Package: graphicx 2014/10/28 v1.0g Enhanced LaTeX Graphics (DPC,SPQR)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty
|
||||
Package: keyval 2014/10/28 v1.15 key=value parser (DPC)
|
||||
\KV@toks@=\toks14
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
|
||||
Package: graphics 2016/01/03 v1.0q Standard LaTeX Graphics (DPC,SPQR)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty
|
||||
Package: trig 2016/01/03 v1.10 sin cos tan (DPC)
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/latexconfig/graphics.cfg
|
||||
File: graphics.cfg 2010/04/23 v1.9 graphics configuration of TeX Live
|
||||
)
|
||||
Package graphics Info: Driver file: pdftex.def on input line 95.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/pdftex-def/pdftex.def
|
||||
File: pdftex.def 2011/05/27 v0.06d Graphics/color for pdfTeX
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/infwarerr.sty
|
||||
Package: infwarerr 2010/04/08 v1.3 Providing info/warning/error messages (HO)
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ltxcmds.sty
|
||||
Package: ltxcmds 2011/11/09 v1.22 LaTeX kernel commands for general use (HO)
|
||||
)
|
||||
\Gread@gobject=\count87
|
||||
))
|
||||
\Gin@req@height=\dimen103
|
||||
\Gin@req@width=\dimen104
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/tools/tabularx.sty
|
||||
Package: tabularx 2014/10/28 v2.10 `tabularx' package (DPC)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/tools/array.sty
|
||||
Package: array 2014/10/28 v2.4c Tabular extension package (FMi)
|
||||
\col@sep=\dimen105
|
||||
\extrarowheight=\dimen106
|
||||
\NC@list=\toks15
|
||||
\extratabsurround=\skip43
|
||||
\backup@length=\skip44
|
||||
)
|
||||
\TX@col@width=\dimen107
|
||||
\TX@old@table=\dimen108
|
||||
\TX@old@col=\dimen109
|
||||
\TX@target=\dimen110
|
||||
\TX@delta=\dimen111
|
||||
\TX@cols=\count88
|
||||
\TX@ftn=\toks16
|
||||
)
|
||||
\c@definition=\count89
|
||||
|
||||
(./casper_basic_structure.aux)
|
||||
\openout1 = `casper_basic_structure.aux'.
|
||||
|
||||
LaTeX Font Info: Checking defaults for OML/cmm/m/it on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for T1/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OT1/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OMS/cmsy/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OMX/cmex/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for U/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/context/base/supp-pdf.mkii
|
||||
[Loading MPS to PDF converter (version 2006.09.02).]
|
||||
\scratchcounter=\count90
|
||||
\scratchdimen=\dimen112
|
||||
\scratchbox=\box26
|
||||
\nofMPsegments=\count91
|
||||
\nofMParguments=\count92
|
||||
\everyMPshowfont=\toks17
|
||||
\MPscratchCnt=\count93
|
||||
\MPscratchDim=\dimen113
|
||||
\MPnumerator=\count94
|
||||
\makeMPintoPDFobject=\count95
|
||||
\everyMPtoPDFconversion=\toks18
|
||||
) (/usr/share/texlive/texmf-dist/tex/generic/oberdiek/pdftexcmds.sty
|
||||
Package: pdftexcmds 2011/11/29 v0.20 Utility functions of pdfTeX for LuaTeX (HO
|
||||
)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ifluatex.sty
|
||||
Package: ifluatex 2010/03/01 v1.3 Provides the ifluatex switch (HO)
|
||||
Package ifluatex Info: LuaTeX not detected.
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ifpdf.sty
|
||||
Package: ifpdf 2011/01/30 v2.3 Provides the ifpdf switch (HO)
|
||||
Package ifpdf Info: pdfTeX in PDF mode is detected.
|
||||
)
|
||||
Package pdftexcmds Info: LuaTeX not detected.
|
||||
Package pdftexcmds Info: \pdf@primitive is available.
|
||||
Package pdftexcmds Info: \pdf@ifprimitive is available.
|
||||
Package pdftexcmds Info: \pdfdraftmode found.
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/epstopdf-base.sty
|
||||
Package: epstopdf-base 2010/02/09 v2.5 Base part for package epstopdf
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/grfext.sty
|
||||
Package: grfext 2010/08/19 v1.1 Manage graphics extensions (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/kvdefinekeys.sty
|
||||
Package: kvdefinekeys 2011/04/07 v1.3 Define keys (HO)
|
||||
))
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/kvoptions.sty
|
||||
Package: kvoptions 2011/06/30 v3.11 Key value format for package options (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/kvsetkeys.sty
|
||||
Package: kvsetkeys 2012/04/25 v1.16 Key value parser (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/etexcmds.sty
|
||||
Package: etexcmds 2011/02/16 v1.5 Avoid name clashes with e-TeX commands (HO)
|
||||
Package etexcmds Info: Could not find \expanded.
|
||||
(etexcmds) That can mean that you are not using pdfTeX 1.50 or
|
||||
(etexcmds) that some package has redefined \expanded.
|
||||
(etexcmds) In the latter case, load this package earlier.
|
||||
)))
|
||||
Package grfext Info: Graphics extension search list:
|
||||
(grfext) [.png,.pdf,.jpg,.mps,.jpeg,.jbig2,.jb2,.PNG,.PDF,.JPG,.JPE
|
||||
G,.JBIG2,.JB2,.eps]
|
||||
(grfext) \AppendGraphicsExtensions on input line 452.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/latexconfig/epstopdf-sys.cfg
|
||||
File: epstopdf-sys.cfg 2010/07/13 v1.3 Configuration of (r)epstopdf for TeX Liv
|
||||
e
|
||||
))
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <14.4> on input line 14.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <7> on input line 14.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <12> on input line 22.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <8> on input line 22.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <6> on input line 22.
|
||||
|
||||
[1
|
||||
|
||||
{/var/lib/texmf/fonts/map/pdftex/updmap/pdftex.map}]
|
||||
<prepares_commits.png, id=14, 1201.288pt x 346.896pt>
|
||||
File: prepares_commits.png Graphic file (type png)
|
||||
|
||||
<use prepares_commits.png>
|
||||
Package pdftex.def Info: prepares_commits.png used on input line 30.
|
||||
(pdftex.def) Requested size: 401.50146pt x 115.93695pt.
|
||||
|
||||
Overfull \hbox (29.12628pt too wide) in paragraph at lines 30--31
|
||||
[][]
|
||||
[]
|
||||
|
||||
LaTeX Font Info: Try loading font information for OMS+cmr on input line 37.
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/omscmr.fd
|
||||
File: omscmr.fd 2014/09/29 v2.5h Standard LaTeX font definitions
|
||||
)
|
||||
LaTeX Font Info: Font shape `OMS/cmr/m/n' in size <12> not available
|
||||
(Font) Font shape `OMS/cmsy/m/n' tried instead on input line 37.
|
||||
[2 <./prepares_commits.png>] [3]
|
||||
Overfull \hbox (2.44592pt too wide) in paragraph at lines 57--58
|
||||
[]\OT1/cmr/m/n/12 This gives sub-stan-tial gains in im-ple-men-ta-tion sim-plic
|
||||
-ity, be-cause it means
|
||||
[]
|
||||
|
||||
|
||||
Overfull \hbox (1.48117pt too wide) in paragraph at lines 62--63
|
||||
[]\OT1/cmr/bx/n/12 NO[]DBL[]PREPARE\OT1/cmr/m/n/12 : a val-ida-tor can-not pre-
|
||||
pare two dif-fer-ent check-
|
||||
[]
|
||||
|
||||
[4] <conflicting_checkpoints.png, id=28, 634.37pt x 403.5075pt>
|
||||
File: conflicting_checkpoints.png Graphic file (type png)
|
||||
|
||||
<use conflicting_checkpoints.png>
|
||||
Package pdftex.def Info: conflicting_checkpoints.png used on input line 76.
|
||||
(pdftex.def) Requested size: 301.1261pt x 191.5449pt.
|
||||
[5 <./conflicting_checkpoints.png>]
|
||||
<fork_choice_rule.jpeg, id=33, 707.64375pt x 442.65375pt>
|
||||
File: fork_choice_rule.jpeg Graphic file (type jpg)
|
||||
|
||||
<use fork_choice_rule.jpeg>
|
||||
Package pdftex.def Info: fork_choice_rule.jpeg used on input line 88.
|
||||
(pdftex.def) Requested size: 401.50146pt x 251.1535pt.
|
||||
|
||||
Overfull \hbox (29.12628pt too wide) in paragraph at lines 88--89
|
||||
[][]
|
||||
[]
|
||||
|
||||
[6 <./fork_choice_rule.jpeg>] [7]
|
||||
<validator_set_misalignment.png, id=42, 422.57875pt x 283.0575pt>
|
||||
File: validator_set_misalignment.png Graphic file (type png)
|
||||
|
||||
<use validator_set_misalignment.png>
|
||||
Package pdftex.def Info: validator_set_misalignment.png used on input line 117.
|
||||
|
||||
(pdftex.def) Requested size: 250.93842pt x 168.09088pt.
|
||||
[8]
|
||||
<CommitsSync.png, id=46, 422.57875pt x 373.395pt>
|
||||
File: CommitsSync.png Graphic file (type png)
|
||||
<use CommitsSync.png>
|
||||
Package pdftex.def Info: CommitsSync.png used on input line 127.
|
||||
(pdftex.def) Requested size: 301.1261pt x 266.08658pt.
|
||||
|
||||
[9 <./validator_set_misalignment.png (PNG copy)>] [10 <./CommitsSync.png>]
|
||||
No file casper_basic_structure.bbl.
|
||||
[11] (./casper_basic_structure.aux) )
|
||||
Here is how much of TeX's memory you used:
|
||||
1637 strings out of 494953
|
||||
23600 string characters out of 6180977
|
||||
80571 words of memory out of 5000000
|
||||
4915 multiletter control sequences out of 15000+600000
|
||||
9456 words of font info for 33 fonts, out of 8000000 for 9000
|
||||
14 hyphenation exceptions out of 8191
|
||||
37i,6n,23p,1062b,181s stack positions out of 5000i,500n,10000p,200000b,80000s
|
||||
</usr/share/texlive/texmf-dist/fonts/type1
|
||||
/public/amsfonts/cm/cmbx10.pfb></usr/share/texlive/texmf-dist/fonts/type1/publi
|
||||
c/amsfonts/cm/cmbx12.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsf
|
||||
onts/cm/cmmi12.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/c
|
||||
m/cmmi8.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr10
|
||||
.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr12.pfb></
|
||||
usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr17.pfb></usr/sha
|
||||
re/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr8.pfb></usr/share/texli
|
||||
ve/texmf-dist/fonts/type1/public/amsfonts/cm/cmsy10.pfb></usr/share/texlive/tex
|
||||
mf-dist/fonts/type1/public/amsfonts/cm/cmsy8.pfb></usr/share/texlive/texmf-dist
|
||||
/fonts/type1/public/amsfonts/cm/cmti12.pfb>
|
||||
Output written on casper_basic_structure.pdf (11 pages, 360532 bytes).
|
||||
PDF statistics:
|
||||
93 PDF objects out of 1000 (max. 8388607)
|
||||
60 compressed objects within 1 object stream
|
||||
0 named destinations out of 1000 (max. 500000)
|
||||
26 words of extra memory for PDF output out of 10000 (max. 10000000)
|
||||
|
||||
|
|
@ -1,144 +0,0 @@
|
|||
\title{Casper the Friendly Finality Gadget: Basic Structure}
|
||||
\author{
|
||||
Vitalik Buterin \\
|
||||
Ethereum Foundation
|
||||
}
|
||||
\date{\today}
|
||||
|
||||
\documentclass[12pt]{article}
|
||||
\usepackage{graphicx}
|
||||
\usepackage{tabularx}
|
||||
\newtheorem{definition}{Definition}
|
||||
|
||||
\begin{document}
|
||||
\maketitle
|
||||
\begin{abstract}
|
||||
We give an introduction to the consensus algorithm details of Casper: the Friendly Finality Gadget, as an overlay on an existing proof of work blockchain such as Ethereum. Byzantine fault tolerance analysis is included, but economic incentive analysis is out of scope.
|
||||
\end{abstract}
|
||||
|
||||
\section{Principles}
|
||||
Casper the Friendly Finality Gadget is designed as an overlay that must be built on top of some kind of ``proposal mechanism'' - a mechanism which ``proposes'' blocks which the Casper mechanism can then set in stone by ``finalizing'' them. The Casper mechanism depends on the proposal mechanism for liveness, but not safety; that is, if the proposal mechanism is entirely corrupted and controlled by adversaries, then the adversaries can prevent Casper from finalizing any blocks, but cannot cause a safety failure in Casper; that is, they cannot force Casper to finalize two conflicting blocks.
|
||||
|
||||
The base mechanism is heavily inspired by partially synchronous systems such as Tendermine [cite] and PBFT [cite], and thus has $\frac{1}{3}$ Byzantine fault tolerance and is safe under asynchrony and dependent on the proposal mechanism for liveness. We later introduce a modification which increases Byzantine fault tolerance to $\frac{1}{2}$, with the proviso that attackers with size $\frac{1}{3} < x < \frac{1}{2}$ can delay new blocks being finalized by some period of time $D$ (think $D \approx$ 3 weeks), at the cost of a ``tradeoff synchrony assumption'' where fault tolerance decreases as network latency goes up, decreasing to potentially zero when network latency reaches $D$.
|
||||
|
||||
In the Casper Phase 1 implementation for Ethereum, the ``proposal mechanism'' is the existing proof of work chain, modified to have a greatly reduced block reward because the chain no longer relies as heavily on proof of work for security, and we describe how the Casper mechanism, and fork choice rule, can be ``overlaid'' onto the proof of work mechanism in order to add Casper's guarantees.
|
||||
|
||||
\section{Introduction, Protocol I}
|
||||
|
||||
In the Casper protocol, there exists a set of validators, and in each \textit{epoch} (see below) validators have the ability to send two kinds of messages: $$[PREPARE, epoch, hash, epoch_{source}, hash_{source}]$$ and $$[COMMIT, epoch, hash]$$
|
||||
|
||||
\includegraphics[width=400px]{prepares_commits.png}
|
||||
|
||||
An \textit{epoch} is a period of 100 blocks; epoch $n$ begins at block $n * 100$ and ends at block $n * 100 + 99$. A \textit{checkpoint for epoch $n$} is a block with number $n * 100 - 1$; in a smoothly running blockchain there will usually be only one checkpoint per epoch, but due to natural network latency or deliberate attacks there may be multiple competing checkpoints during some epochs. The \textit{parent checkpoint} of a checkpoint is the 100th ancestor of the checkpoint block, and an \textit{ancestor checkpoint} of a checkpoint is either the parent checkpoint, or an ancestor checkpoint of the parent checkpoint.
|
||||
|
||||
We define the \textit{ancestry hash} of a checkpoint as follows:
|
||||
|
||||
\begin{itemize}
|
||||
\item The ancestry hash of the implied ``genesis checkpoint'' of epoch 0 is thirty two zero bytes.
|
||||
\item The ancestry hash of any other checkpoint is the keccak256 hash of the ancestry hash of its parent checkpoint concatenated with the hash of the checkpoint.
|
||||
\end{itemize}
|
||||
|
||||
Ancestry hashes thus form a direct hash chain, and otherwise have a one-to-one correspondence with checkpoint hashes.
|
||||
|
||||
During epoch $n$, validators are expected to send prepare and commit messages specifying $n$ as their $epoch$, and the ancestry hash of some checkpoint for epoch $n$ as their $hash$. Prepare messages are expected to specify as $hash_{source}$ a checkpoint for any previous epoch which is an ancestor of the $hash$, and which is \textit{justified} (see below), and the $epoch_{source}$ is expected to be the epoch of that checkpoint.
|
||||
|
||||
Each validator has a \textit{deposit size}; when a validator joins their deposit size is equal to the number of coins that they deposited, and from there on each validator's deposit size rises and falls as the validator receives rewards and penalties. For the rest of this paper, when we say ``$\frac{2}{3}$ of validators", we are referring to a \textit{deposit-weighted} fraction; that is, a set of validators whose combined deposit size equals to at least $\frac{2}{3}$ of the total deposit size of the entire set of validators. We also use ``$\frac{2}{3}$ commits" as shorthand for ``commits from $\frac{2}{3}$ of validators". At first, we will consider the set of validators, and their deposit sizes, static, but in later sections we will introduce the notion of validator set changes.
|
||||
|
||||
If, during an epoch $e$, for some specific ancestry hash $h$, for any specific ($epoch_{source}, hash_{source}$ pair), there exist $\frac{2}{3}$ prepares of the form $$[PREPARE, e, h, epoch_{source}, hash_{source}]$$, then $h$ is considered \textit{justified}. If $\frac{2}{3}$ commits are sent of the form $$[COMMIT, e, h]$$ then $h$ is considered \textit{finalized}.
|
||||
|
||||
We also add the following requirements:
|
||||
|
||||
\begin{itemize}
|
||||
\item For a checkpoint to be finalized, it must be justified.
|
||||
\item For a checkpoint to be justified, the $hash_{source}$ used to justify it must itself be justified.
|
||||
\item Prepare and commit messages are only accepted as part of blocks; that is, for a client to see $\frac{2}{3}$ commits of some hash, they must receive a block such that in the chain terminating at that block $\frac{2}{3}$ commits for that hash have been included and processed.
|
||||
\end{itemize}
|
||||
|
||||
This gives substantial gains in implementation simplicity, because it means that we can now have a fork choice rule where the ``score'' of a block only depends on the block and its children, putting it into a similar category as more traditional PoW-based fork choice rules such as the longest chain rule and GHOST. However, this fork choice rule is also \textit{finality-bearing}: there exists a ``finality'' mechanism that has the property that (i) the fork choice rule always prefers finalized blocks over non-finalized competing blocks, and (ii) it is impossible for two incompatible checkpoints to be finalized unless at least $\frac{1}{3}$ of the validators violated a \textit{slashing condition} (see below).
|
||||
|
||||
There are two slashing conditions:
|
||||
|
||||
\begin{enumerate}
|
||||
\item \textbf{NO\_DBL\_PREPARE}: a validator cannot prepare two different checkpoints for the same epoch.
|
||||
\item \textbf{PREPARE\_COMMIT\_CONSISTENCY}: if a validator has made a commit with epoch $n$, they cannot make a prepare with $epoch > n$ and $epoch_{source} < n$.
|
||||
\end{enumerate}
|
||||
|
||||
Earlier versions of Casper had four slashing conditions, but we can reduce to two because of the three modifications above; they ensure that blocks will not register commits or prepares that violate the other two conditions.
|
||||
|
||||
\section{Proof Sketch of Safety and Plausible Liveness}
|
||||
|
||||
We give a proof sketch of two properties of this scheme: \textit{accountable safety} and \textit{plausible liveness}. Accountable safety means that two conflicting checkpoints cannot be finalized unless at least $\frac{1}{3}$ of validators violate a slashing condition. Honest validators will not violate slashing conditions, so this implies the usual Byzantine fault tolerance safety property, but expressing this in terms of slashing conditions means that we are actually proving a stronger claim: if two conflicting checkpoints get finalized, then at least $\frac{1}{3}$ of validators were malicious, \textit{and we know whom to blame, and so we can maximally penalize them in order to make such faults expensive}.
|
||||
|
||||
Plausible liveness means that it is always possible for $\frac{2}{3}$ of honest validators to finalize a new checkpoint, regardless of what previous events took place.
|
||||
|
||||
Suppose that two conflicting checkpoints $A$ (epoch $e_A$) and $B$ (epoch $e_B$) are finalized.
|
||||
|
||||
\includegraphics[width=300px]{conflicting_checkpoints.png}
|
||||
|
||||
This implies $\frac{2}{3}$ commits and $\frac{2}{3}$ prepares in epochs $e_A$ and $e_B$. In the trivial case where $e_A = e_B$, this implies that some intersection of $\frac{1}{3}$ of validators must have violated \textbf{NO\_DBL\_PREPARE}. In other cases, there must exist two chains $e_A > e_A^1 > e_A^2 > ... > G$ and $e_B > e_B^1 > e_B^2 > ... > G$ of justified checkpoints, both terminating at the genesis. Suppose without loss of generality that $e_A > e_B$. Then, there must be some $e_A^i$ that either $e_A^i = e_B$ or $e_A^i > e_B > e_A^{i+1}$. In the first case, since $A^i$ and $B$ both have $\frac{2}{3}$ prepares, at least $\frac{1}{3}$ of validators violated \textbf{NO\_DBL\_PREPARE}. Otherwise, $B$ has $\frac{2}{3}$ commits and there exist $\frac{2}{3}$ prepares with $epoch > B$ and $epoch_{source} < B$, so at least $\frac{1}{3}$ of validators violated \textbf{PREPARE\_COMMIT\_CONSISTENCY}. This proves accountable safety.
|
||||
|
||||
Now, we prove plausible liveness. Suppose that all existing validators have sent some sequence of prepare and commit messages. Let $M$ with epoch $e_M$ be the highest-epoch checkpoint that was justified. Honest validators have not committed on any block which is not justified. Hence, neither slashing condition stops them from making prepares on a child of $M$, using $e_M$ as $epoch_{source}$, and then committing this child.
|
||||
|
||||
\section{Fork Choice Rule}
|
||||
|
||||
The mechanism described above ensures \textit{plausible liveness}; however, it by itself does not ensure \textit{actual liveness} - that is, while the mechanism cannot get stuck in the strict sense, it could still enter a scenario where the proposal mechanism (i.e. the proof of work chain) gets into a state where it never ends up creating a checkpoint that could get finalized.
|
||||
|
||||
Here is one possible example:
|
||||
|
||||
\includegraphics[width=400px]{fork_choice_rule.jpeg}
|
||||
|
||||
In this case, $HASH1$ or any descendant thereof cannot be finalized without slashing $\frac{1}{6}$ of validators. However, miners on a proof of work chain would interpret $HASH1$ as the head and forever keep mining descendants of it, ignoring the chain based on $HASH0'$ which actually could get finalized.
|
||||
|
||||
In fact, when \textit{any} checkpoint gets $k > \frac{1}{3}$ commits, no conflicting checkpoint can get finalized without $k - \frac{1}{3}$ of validators getting slashed. This necessitates modifying the fork choice rule used by participants in the underlying proposal mechanism (as well as users and validators): instead of blindly following a longest-chain rule, there needs to be an overriding rule that (i) finalized checkpoints are favored, and (ii) when there are no further finalized checkpoints, checkpoints with more (justified) commits are favored.
|
||||
|
||||
One complete description of such a rule would be:
|
||||
|
||||
\begin{enumerate}
|
||||
\item Start with HEAD equal to the genesis of the chain.
|
||||
\item Select the descendant checkpoint of HEAD with the most commits (only justified checkpoints are admissible)
|
||||
\item Repeat (2) until no descendant with commits exists.
|
||||
\item Choose the longest proof of work chain from there.
|
||||
\end{enumerate}
|
||||
|
||||
The commit-following part of this rule can be viewed in some ways as mirroring the "greegy heaviest observed subtree" (GHOST) rule that has been proposed for proof of work chains [cite]. The symmetry is as follows. In GHOST, a node starts with the head at the genesis, then begins to move forward down the chain, and if it encounters a block with multiple children then it chooses the child that has the larger quantity of work built on top of it (including the child block itself and its descendants).
|
||||
|
||||
In this algorithm, we follow a similar approach, except we repeatedly seek the child that comes the closest to achieving finality. Commits on a descendant are implicitly commits on all of its ancestors, and so if a given descendant of a given block has more commits than any other descendant, then we know that all children along the chain from the head to this descendant are closer to finality than any of their siblings; hence, looking for the \textit{descendant} with the most commits and not just the \textit{child} replicates the GHOST principle most faithfully. Finalizing a checkpoint requires $\frac{2}{3}$ commits within a \textit{single} epoch, and so we do not try to sum up commits across epochs and instead simply take the maximum.
|
||||
|
||||
This rule ensures that if there is a checkpoint such that no conflicting checkpoint can be finalized without at least some validators violating slashing conditions, then this is the checkpoint that will be viewed as the ``head'' and thus that validators will try to commit on.
|
||||
|
||||
\section{Dynamic Validator Sets}
|
||||
|
||||
In an open protocol, the validator set needs to be able to change; old validators need to be able to withdraw, and new validators need to be able to enter. To accomplish this end, we define a variable kept track of in the state called the \textit{dynasty} counter. When a user sends a ``deposit'' transaction to become a validator, if this transaction is included in dynasty $n$, then the validator will be \textit{inducted} in dynasty $n+2$. The dynasty counter is incremented when the chain detects that the checkpoint of the current epoch that is part of its own history has been finalized (that is, the checkpoint of epoch $e$ must be finalized during epoch $e$, and the chain must learn about this before epoch $e$ ends). In simpler terms, when a user sends a ``deposit'' transaction, they need to wait for the transaction to be finalized, and then they need to wait again for that epoch to be finalized; after this, they become part of the validator set. We call such a validator's \textit{start dynasty} $n+2$.
|
||||
|
||||
For a validator to leave, they must send a ``withdraw'' message. If their withdraw message gets included during dynasty $n$, the validator similarly leaves the validator set during dynasty $n+2$; we call $n+2$ their \textit{end dynasty}. When a validator withdraws, their deposit is locked for four months before they can take their money out; if they are caught violating a slashing condition within that time then their deposit is forfeited.
|
||||
|
||||
For a checkpoint to be justified, it must be prepared by a set of validators which contains (i) at least $\frac{2}{3}$ of the current dynasty (that is, validators with $startDynasty \le curDynasty < endDynasty$), and (ii) at least $\frac{2}{3}$ of the previous dynasty (that is, validators with $startDynasty \le curDynasty - 1 < endDynasty$. Finalization with commits works similarly. The current and previous dynasties will usually mostly overlap; but in cases where they substantially diverge this ``stitching'' mechanism ensures that dynasty divergences do not lead to situations where a finality reversion or other failure can happen because different messages are signed by different validator sets and so equivocation is avoided.
|
||||
|
||||
\includegraphics[width=250px]{validator_set_misalignment.png}
|
||||
|
||||
\section{Mass Crash Failure Recovery}
|
||||
|
||||
Suppose that more than one third of validators crash-fail at the same time; that is, they either are no longer connected to the network due to a network partition, or their computers fail, or they do this as a malicious attack. Then, no checkpoint will be able to get finalized.
|
||||
|
||||
We can recover from this by instituting a rule that validators who do not prepare or commit for a long time start to see their deposit sizes decrease (depending on the desired economic incentives this can be either a compulsory partial withdrawal or an outright confiscation), until eventually their deposit sizes decrease low enough that the validators that \textit{are} preparing and committing are once again a $\frac{2}{3}$ supermajority.
|
||||
|
||||
Note that this does introduce the possibility of two conflicting checkpoints being finalized, with validators only losing money on one of the two checkpoints:
|
||||
|
||||
\includegraphics[width=300px]{CommitsSync.png}
|
||||
|
||||
If the goal is simply to achieve maximally close to 50\% fault tolerance, then clients should simply favor the finalized checkpoint that they received earlier. However, if clients are also interested in defeating 51\% censorship attacks, then they may want to at least sometimes choose the minority chain. All forms of ``51\% attacks'' can thus be resolved fairly cleanly via ``user-activated soft forks'' that reject what would normally be the dominant chain. Particularly, note that finalizing even one block on the dominant chain precludes the attacking validators from preparing on the minority chain because of \textbf{PREPARE\_COMMIT\_CONSISTENCY}, at least until their balances decrease to the point where the minority can commit, so such a fork would also serve the function of costing the majority attacker a very large portion of their deposits.
|
||||
|
||||
\section{Conclusions}
|
||||
|
||||
This introduces the basic workings of Casper the Friendly Finality Gadget's prepare and commit mechanism and fork choice rule, in the context of Byzantine fault tolerance analysis. Separate papers will serve the role of explaining and analyzing incentives inside of Casper, and the different ways that they can be parametrized and the consequences of these paramtrizations.
|
||||
|
||||
\section{References}
|
||||
\bibliographystyle{abbrv}
|
||||
\bibliography{main}
|
||||
\begin{itemize}
|
||||
\item Aviv Zohar and Yonatan Sompolinsky, ``Fast Money Grows on Trees, not Chains'': https://eprint.iacr.org/2013/881.pdf
|
||||
\item Jae Kwon, ``Tendermint'': http://tendermint.org/tendermint.pdf
|
||||
\item Miguel Castro and Barbara Liskov, ``Practical Byzantine Fault Tolerance'': http://pmg.csail.mit.edu/papers/osdi99.pdf
|
||||
\end{itemize}
|
||||
|
||||
\end{document}
|
||||
|
|
@ -1,12 +0,0 @@
|
|||
\relax
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {1}Introduction}{1}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {2}Rewards and Penalties}{3}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {3}Claims}{5}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {4}Individual choice analysis}{5}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {5}Collective choice model}{6}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {6}Griefing factor analysis}{7}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {7}Pools}{10}}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {8}Conclusions}{11}}
|
||||
\bibstyle{abbrv}
|
||||
\bibdata{main}
|
||||
\@writefile{toc}{\contentsline {section}{\numberline {9}References}{12}}
|
||||
|
|
@ -1,242 +0,0 @@
|
|||
This is pdfTeX, Version 3.14159265-2.6-1.40.16 (TeX Live 2015/Debian) (preloaded format=pdflatex 2017.6.27) 25 JUL 2017 00:09
|
||||
entering extended mode
|
||||
restricted \write18 enabled.
|
||||
%&-line parsing enabled.
|
||||
**casper_economics_basic.tex
|
||||
(./casper_economics_basic.tex
|
||||
LaTeX2e <2016/02/01>
|
||||
Babel <3.9q> and hyphenation patterns for 3 language(s) loaded.
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
|
||||
Document Class: article 2014/09/29 v1.4h Standard LaTeX document class
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/size12.clo
|
||||
File: size12.clo 2014/09/29 v1.4h Standard LaTeX file (size option)
|
||||
)
|
||||
\c@part=\count79
|
||||
\c@section=\count80
|
||||
\c@subsection=\count81
|
||||
\c@subsubsection=\count82
|
||||
\c@paragraph=\count83
|
||||
\c@subparagraph=\count84
|
||||
\c@figure=\count85
|
||||
\c@table=\count86
|
||||
\abovecaptionskip=\skip41
|
||||
\belowcaptionskip=\skip42
|
||||
\bibindent=\dimen102
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
|
||||
Package: graphicx 2014/10/28 v1.0g Enhanced LaTeX Graphics (DPC,SPQR)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty
|
||||
Package: keyval 2014/10/28 v1.15 key=value parser (DPC)
|
||||
\KV@toks@=\toks14
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
|
||||
Package: graphics 2016/01/03 v1.0q Standard LaTeX Graphics (DPC,SPQR)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty
|
||||
Package: trig 2016/01/03 v1.10 sin cos tan (DPC)
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/latexconfig/graphics.cfg
|
||||
File: graphics.cfg 2010/04/23 v1.9 graphics configuration of TeX Live
|
||||
)
|
||||
Package graphics Info: Driver file: pdftex.def on input line 95.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/pdftex-def/pdftex.def
|
||||
File: pdftex.def 2011/05/27 v0.06d Graphics/color for pdfTeX
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/infwarerr.sty
|
||||
Package: infwarerr 2010/04/08 v1.3 Providing info/warning/error messages (HO)
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ltxcmds.sty
|
||||
Package: ltxcmds 2011/11/09 v1.22 LaTeX kernel commands for general use (HO)
|
||||
)
|
||||
\Gread@gobject=\count87
|
||||
))
|
||||
\Gin@req@height=\dimen103
|
||||
\Gin@req@width=\dimen104
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/tools/tabularx.sty
|
||||
Package: tabularx 2014/10/28 v2.10 `tabularx' package (DPC)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/tools/array.sty
|
||||
Package: array 2014/10/28 v2.4c Tabular extension package (FMi)
|
||||
\col@sep=\dimen105
|
||||
\extrarowheight=\dimen106
|
||||
\NC@list=\toks15
|
||||
\extratabsurround=\skip43
|
||||
\backup@length=\skip44
|
||||
)
|
||||
\TX@col@width=\dimen107
|
||||
\TX@old@table=\dimen108
|
||||
\TX@old@col=\dimen109
|
||||
\TX@target=\dimen110
|
||||
\TX@delta=\dimen111
|
||||
\TX@cols=\count88
|
||||
\TX@ftn=\toks16
|
||||
)
|
||||
\c@definition=\count89
|
||||
|
||||
(./casper_economics_basic.aux)
|
||||
\openout1 = `casper_economics_basic.aux'.
|
||||
|
||||
LaTeX Font Info: Checking defaults for OML/cmm/m/it on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for T1/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OT1/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OMS/cmsy/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for OMX/cmex/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
LaTeX Font Info: Checking defaults for U/cmr/m/n on input line 13.
|
||||
LaTeX Font Info: ... okay on input line 13.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/context/base/supp-pdf.mkii
|
||||
[Loading MPS to PDF converter (version 2006.09.02).]
|
||||
\scratchcounter=\count90
|
||||
\scratchdimen=\dimen112
|
||||
\scratchbox=\box26
|
||||
\nofMPsegments=\count91
|
||||
\nofMParguments=\count92
|
||||
\everyMPshowfont=\toks17
|
||||
\MPscratchCnt=\count93
|
||||
\MPscratchDim=\dimen113
|
||||
\MPnumerator=\count94
|
||||
\makeMPintoPDFobject=\count95
|
||||
\everyMPtoPDFconversion=\toks18
|
||||
) (/usr/share/texlive/texmf-dist/tex/generic/oberdiek/pdftexcmds.sty
|
||||
Package: pdftexcmds 2011/11/29 v0.20 Utility functions of pdfTeX for LuaTeX (HO
|
||||
)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ifluatex.sty
|
||||
Package: ifluatex 2010/03/01 v1.3 Provides the ifluatex switch (HO)
|
||||
Package ifluatex Info: LuaTeX not detected.
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/ifpdf.sty
|
||||
Package: ifpdf 2011/01/30 v2.3 Provides the ifpdf switch (HO)
|
||||
Package ifpdf Info: pdfTeX in PDF mode is detected.
|
||||
)
|
||||
Package pdftexcmds Info: LuaTeX not detected.
|
||||
Package pdftexcmds Info: \pdf@primitive is available.
|
||||
Package pdftexcmds Info: \pdf@ifprimitive is available.
|
||||
Package pdftexcmds Info: \pdfdraftmode found.
|
||||
)
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/epstopdf-base.sty
|
||||
Package: epstopdf-base 2010/02/09 v2.5 Base part for package epstopdf
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/grfext.sty
|
||||
Package: grfext 2010/08/19 v1.1 Manage graphics extensions (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/kvdefinekeys.sty
|
||||
Package: kvdefinekeys 2011/04/07 v1.3 Define keys (HO)
|
||||
))
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/oberdiek/kvoptions.sty
|
||||
Package: kvoptions 2011/06/30 v3.11 Key value format for package options (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/kvsetkeys.sty
|
||||
Package: kvsetkeys 2012/04/25 v1.16 Key value parser (HO)
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/generic/oberdiek/etexcmds.sty
|
||||
Package: etexcmds 2011/02/16 v1.5 Avoid name clashes with e-TeX commands (HO)
|
||||
Package etexcmds Info: Could not find \expanded.
|
||||
(etexcmds) That can mean that you are not using pdfTeX 1.50 or
|
||||
(etexcmds) that some package has redefined \expanded.
|
||||
(etexcmds) In the latter case, load this package earlier.
|
||||
)))
|
||||
Package grfext Info: Graphics extension search list:
|
||||
(grfext) [.png,.pdf,.jpg,.mps,.jpeg,.jbig2,.jb2,.PNG,.PDF,.JPG,.JPE
|
||||
G,.JBIG2,.JB2,.eps]
|
||||
(grfext) \AppendGraphicsExtensions on input line 452.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/latexconfig/epstopdf-sys.cfg
|
||||
File: epstopdf-sys.cfg 2010/07/13 v1.3 Configuration of (r)epstopdf for TeX Liv
|
||||
e
|
||||
))
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <14.4> on input line 14.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <7> on input line 14.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <10.95> on input line 16.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <8> on input line 16.
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <6> on input line 16.
|
||||
|
||||
Overfull \hbox (0.3523pt too wide) in paragraph at lines 16--17
|
||||
[]\OT1/cmr/m/n/10.95 We give an in-tro-duc-tion to the in-cen-tives in the Casp
|
||||
er the Friendly
|
||||
[]
|
||||
|
||||
LaTeX Font Info: External font `cmex10' loaded for size
|
||||
(Font) <12> on input line 20.
|
||||
[1
|
||||
|
||||
{/var/lib/texmf/fonts/map/pdftex/updmap/pdftex.map}]
|
||||
LaTeX Font Info: Try loading font information for OMS+cmr on input line 29.
|
||||
|
||||
(/usr/share/texlive/texmf-dist/tex/latex/base/omscmr.fd
|
||||
File: omscmr.fd 2014/09/29 v2.5h Standard LaTeX font definitions
|
||||
)
|
||||
LaTeX Font Info: Font shape `OMS/cmr/m/n' in size <12> not available
|
||||
(Font) Font shape `OMS/cmsy/m/n' tried instead on input line 29.
|
||||
[2] [3] [4]
|
||||
Overfull \hbox (10.7546pt too wide) in paragraph at lines 80--81
|
||||
[]\OT1/cmr/m/n/12 Hence, the PRE-PARE[]COMMIT[]CONSISTENCY slash-ing con-di-tio
|
||||
n poses
|
||||
[]
|
||||
|
||||
|
||||
Overfull \hbox (5.39354pt too wide) in paragraph at lines 82--83
|
||||
[]\OT1/cmr/m/n/12 We are as-sum-ing that there are $[]$ pre-pares for $(\OML/cm
|
||||
m/m/it/12 e; H; epoch[]; hash[]\OT1/cmr/m/n/12 )$,
|
||||
[]
|
||||
|
||||
[5] [6]
|
||||
Overfull \hbox (15.85455pt too wide) in paragraph at lines 105--105
|
||||
[]\OT1/cmr/m/n/12 Now, we need to show that, for any given to-tal de-posit size
|
||||
, $[]$
|
||||
[]
|
||||
|
||||
[7]
|
||||
Underfull \hbox (badness 3291) in paragraph at lines 147--147
|
||||
[]|\OT1/cmr/m/n/12 Amount lost by at-
|
||||
[]
|
||||
|
||||
|
||||
Overfull \hbox (17.62482pt too wide) in paragraph at lines 147--148
|
||||
[][]
|
||||
[]
|
||||
|
||||
[8] [9] [10] [11]
|
||||
No file casper_economics_basic.bbl.
|
||||
[12] (./casper_economics_basic.aux) )
|
||||
Here is how much of TeX's memory you used:
|
||||
1613 strings out of 494953
|
||||
22986 string characters out of 6180977
|
||||
84568 words of memory out of 5000000
|
||||
4898 multiletter control sequences out of 15000+600000
|
||||
10072 words of font info for 35 fonts, out of 8000000 for 9000
|
||||
14 hyphenation exceptions out of 8191
|
||||
37i,10n,23p,1059b,181s stack positions out of 5000i,500n,10000p,200000b,80000s
|
||||
</usr/share/texlive/texmf-dist/fonts/type1
|
||||
/public/amsfonts/cm/cmbx10.pfb></usr/share/texlive/texmf-dist/fonts/type1/publi
|
||||
c/amsfonts/cm/cmbx12.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsf
|
||||
onts/cm/cmex10.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/c
|
||||
m/cmmi12.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmmi
|
||||
6.pfb></usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmmi8.pfb><
|
||||
/usr/share/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr10.pfb></usr/sh
|
||||
are/texlive/texmf-dist/fonts/type1/public/amsfonts/cm/cmr12.pfb></usr/share/tex
|
||||
live/texmf-dist/fonts/type1/public/amsfonts/cm/cmr17.pfb></usr/share/texlive/te
|
||||
xmf-dist/fonts/type1/public/amsfonts/cm/cmr8.pfb></usr/share/texlive/texmf-dist
|
||||
/fonts/type1/public/amsfonts/cm/cmsy10.pfb></usr/share/texlive/texmf-dist/fonts
|
||||
/type1/public/amsfonts/cm/cmsy8.pfb></usr/share/texlive/texmf-dist/fonts/type1/
|
||||
public/amsfonts/cm/cmti12.pfb>
|
||||
Output written on casper_economics_basic.pdf (12 pages, 181449 bytes).
|
||||
PDF statistics:
|
||||
95 PDF objects out of 1000 (max. 8388607)
|
||||
67 compressed objects within 1 object stream
|
||||
0 named destinations out of 1000 (max. 500000)
|
||||
1 words of extra memory for PDF output out of 10000 (max. 10000000)
|
||||
|
||||
|
|
@ -1,201 +0,0 @@
|
|||
\title{Incentives in Casper the Friendly Finality Gadget}
|
||||
\author{
|
||||
Vitalik Buterin \\
|
||||
Ethereum Foundation
|
||||
}
|
||||
\date{\today}
|
||||
|
||||
\documentclass[12pt]{article}
|
||||
\usepackage{graphicx}
|
||||
\usepackage{tabularx}
|
||||
\newtheorem{definition}{Definition}
|
||||
|
||||
\begin{document}
|
||||
\maketitle
|
||||
\begin{abstract}
|
||||
We give an introduction to the incentives in the Casper the Friendly Finality Gadget protocol, and show how the protocol behaves under individual choice analysis, collective choice analysis and griefing factor analysis. We define a ``protocol utility function'' that represents the protocol's view of how well it is being executed, and show the connection between the incentive structure that we present and the utility function. We show that (i) the protocol is a Nash equilibrium assuming any individual validator's deposit makes up less than $\frac{1}{3}$ of the total, (ii) in a collective choice model, where all validators are controlled by one actor, harming protocol utility hurts the cartel's revenue, and there is an upper bound on the ratio between the reduction in protocol utility from an attack and the cost to the attacker, and (iii) the griefing factor can be bounded above by $1$, though we will prefer an alternative model that bounds the griefing factor at $2$ in exchange for other benefits.
|
||||
\end{abstract}
|
||||
|
||||
\section{Introduction}
|
||||
In the Casper protocol, there is a set of validators, and in each epoch validators have the ability to send two kinds of messages: $$[PREPARE, epoch, hash, epoch_{source}, hash_{source}]$$ and $$[COMMIT, epoch, hash]$$
|
||||
|
||||
Each validator has a \textit{deposit size}; when a validator joins their deposit size is equal to the number of coins that they deposited, and from there on each validator's deposit size rises and falls as the validator receives rewards and penalties. For the rest of this paper, when we say ``$\frac{2}{3}$ of validators", we are referring to a \textit{deposit-weighted} fraction; that is, a set of validators whose combined deposit size equals to at least $\frac{2}{3}$ of the total deposit size of the entire set of validators. We also use ``$\frac{2}{3}$ commits" as shorthand for ``commits from $\frac{2}{3}$ of validators".
|
||||
|
||||
If, during an epoch $e$, for some specific checkpoint hash $h$, $\frac{2}{3}$ prepares are sent of the form $$[PREPARE, e, h, epoch_{source}, hash_{source}]$$ with some specific $epoch_{source}$ and some specific $hash_{source}$, then $h$ is considered \textit{justified}. If $\frac{2}{3}$ commits are sent of the form $$[COMMIT, e, h]$$ then $h$ is considered \textit{finalized}. The $hash$ is the block hash of the block at the start of the epoch, so a $hash$ being finalized means that that block, and all of its ancestors, are also finalized. An ``ideal execution'' of the protocol is one where, during every epoch, every validator prepares and commits some block hash at the start of that epoch, specifying the same $epoch_{source}$ and $hash_{source}$. We want to try to create incentives to encourage this ideal execution.
|
||||
|
||||
Possible deviations from this ideal execution that we want to minimize or avoid include:
|
||||
|
||||
\begin{itemize}
|
||||
\item Any of the four slashing conditions get violated.
|
||||
\item During some epoch, we do not get $\frac{2}{3}$ commits for the $hash$ that received $\frac{2}{3}$ prepares.
|
||||
\item During some epoch, we do not get $\frac{2}{3}$ prepares for the same \\ $(h, hash_{source}, epoch_{source})$ combination.
|
||||
\end{itemize}
|
||||
|
||||
From within the view of the blockchain, we only see the blockchain's own history, including messages that were passed in. In a history that contains some blockhash $H$, our strategy will be to reward validators who prepared and committed $H$, and not reward prepares or commits for any hash $H\prime \ne H$. The blockchain state will also keep track of the most recent hash in its own history that received $\frac{2}{3}$ prepares, and only reward prepares whose $epoch_{source}$ and $hash_{source}$ point to this hash. These two techniques will help to ``coordinate'' validators toward preparing and committing a single hash with a single source, as required by the protocol.
|
||||
|
||||
\section{Rewards and Penalties}
|
||||
|
||||
We define the following constants and functions:
|
||||
|
||||
\begin{itemize}
|
||||
\item $BIR(D)$: determines the base interest rate paid to each validator, taking as an input the current total quantity of deposited ether.
|
||||
\item $BP(D, e, LFE)$: determines the ``base penalty constant'' - a value expressed as a percentage rate that is used as the ``scaling factor'' for all penalties; for example, if at the current time $BP(...) = 0.001$, then a penalty of size $1.5$ means a validator loses $0.15\%$ of their deposit. Takes as inputs the current total quantity of deposited ether $D$, the current epoch $e$ and the last finalized epoch $LFE$. Note that in a ``perfect'' protocol execution, $e - LFE$ always equals $1$.
|
||||
\item $NCP$ (``non-commit penalty''): the penalty for not committing, if there was a justified hash which the validator \textit{could} have committed
|
||||
\item $NCCP(\alpha)$ (``non-commit collective penalty''): if $\alpha$ of validators are not seen to have committed during an epoch, and that epoch had a justified hash so any validator \textit{could} have committed, then all validators are charged a penalty proportional to $NCCP(\alpha)$. Must be monotonically increasing, and satisfy $NCCP(0) = 0$.
|
||||
\item $NPP$ (``non-prepare penalty''): the penalty for not preparing
|
||||
\item $NPCP(\alpha)$ (``non-prepare collective penalty''): if $\alpha$ of validators are not seen to have prepared during an epoch, then all validators are charged a penalty proportional to $NCCP(\alpha)$. Must be monotonically increasing, and satisfy $NPCP(0) = 0$.
|
||||
\end{itemize}
|
||||
|
||||
Note that preparing and committing does not guarantee that the validator will not incur $NPP$ and $NCP$; it could be the case that either because of very high network latency or a malicious majority censorship attack, the prepares and commits are not included into the blockchain in time and so the incentivization mechanism does not know about them. For $NPCP$ and $NCCP$ similarly, the $\alpha$ input is the portion of validators whose prepares and commits are \textit{included}, not the portion of validators who \textit{tried to send} prepares and commits.
|
||||
|
||||
When we talk about preparing and committing the ``correct value", we are referring to the $hash$ and $epoch_{source}$ and $hash_{source}$ recommended by the protocol state, as described above.
|
||||
|
||||
We now define the following reward and penalty schedule, which runs every epoch.
|
||||
|
||||
\begin{itemize}
|
||||
\item Let $D$ be the current total quantity of deposited ether, and $e - LFE$ be the number of epochs since the last finalized epoch.
|
||||
\item All validators get a reward of $BIR(D)$ every epoch (eg. if $BIR(D) = 0.0002$ then a validator with $10000$ coins deposited gets a per-epoch reward of $2$ coins)
|
||||
\item If the protocol does not see a prepare from a given validator during the given epoch, they are penalized $BP(D, e, LFE) * NPP$
|
||||
\item If the protocol saw prepares from portion $p_p$ validators during the given epoch, \textit{every} validator is penalized $BP(D, e, LFE) * NPCP(1 - p_p)$
|
||||
\item If the protocol does not see a commit from a given validator during the given epoch, and a prepare was justified so a commit \textit{could have} been seen, they are penalized $BP(D, E, LFE) * NCP$.
|
||||
\item If the protocol saw commits from portion $p_c$ validators during the given epoch, and a prepare was justified so any validator \textit{could have} committed, then \textit{every} validator is penalized $BP(D, e, LFE) * NCCP(1 - p_p)$
|
||||
\end{itemize}
|
||||
|
||||
This is the entirety of the incentivization structure, though without functions and constants defined; we will define these later, attempting as much as possible to derive the specific values from desired objectives and first principles. For now we will only say that all constants are positive and all functions output non-negative values for any input within their range. Additionally, $NPCP(0) = NCCP(0) = 0$ and $NPCP$ and $NCCP$ must both be nondecreasing.
|
||||
|
||||
\section{Claims}
|
||||
|
||||
We seek to prove the following:
|
||||
|
||||
\begin{itemize}
|
||||
\item If each validator has less than $\frac{1}{3}$ of total deposits, then preparing and committing the value suggested by the proposal mechanism is a Nash equilibrium.
|
||||
\item Even if all validators collude, the ratio between the harm incurred by the protocol and the penalties paid by validators is bounded above by some constant. Note that this requires a measure of ``harm incurred by the protocol"; we will discuss this in more detail later.
|
||||
\item The \textit{griefing factor}, the ratio between penalties incurred by validators who are victims of an attack and penalties incurred by the validators that carried out the attack, can be bounded above by 2, even in the case where the attacker holds a majority of the total deposits.
|
||||
\end{itemize}
|
||||
|
||||
\section{Individual choice analysis}
|
||||
|
||||
The individual choice analysis is simple. Suppose that the proposal mechanism selects a hash $H$ to prepare for epoch $e$, and the Casper incentivization mechanism specifies some $epoch_{source}$ and $hash_{source}$. Because, as per definition of the Nash equilibrium, we are assuming that all validators except for one particular validator that we are analyzing is following the equilibrium strategy, we know that $\ge \frac{2}{3}$ of validators prepared in the last epoch and so $epoch_{source} = e - 1$, and $hash_{source}$ is the direct parent of $H$.
|
||||
|
||||
Hence, the PREPARE\_COMMIT\_CONSISTENCY slashing condition poses no barrier to preparing $(e, H, epoch_{source}, hash_{source})$. Since, in epoch $e$, we are assuming that all other validators \textit{will} prepare these values and then commit $H$, we know $H$ will be the hash in the main chain, and so a validator will pay a penalty proportional to $NPP$ (plus a further penalty from their marginal contribution to the $NPCP$ penalty) if they do not prepare $(e, H, epoch_{source}, hash_{source})$, and they can avoid this penalty if they do prepare these values.
|
||||
|
||||
We are assuming that there are $\frac{2}{3}$ prepares for $(e, H, epoch_{source}, hash_{source})$, and so PREPARE\_REQ poses no barrier to committing $H$. Committing $H$ allows a validator to avoid $NCP$ (as well as their marginal contribution to $NCCP$). Hence, there is an economic incentive to commit $H$. This shows that, if the proposal mechanism succeeds at presenting to validators a single primary choice, preparing and committing the value selected by the proposal mechanism is a Nash equilibrium.
|
||||
|
||||
\section{Collective choice model}
|
||||
|
||||
To model the protocol in a collective-choice context, we will first define a \textit{protocol utility function}. The protocol utility function defines ``how well the protocol execution is doing". The protocol utility function cannot be derived mathematically; it can only be conceived and justified intuitively.
|
||||
|
||||
Our protocol utility function is:
|
||||
|
||||
$$U = \sum_{e = 0}^{e_c} -log_2(e - LFE(e)) - M * F$$
|
||||
|
||||
Where:
|
||||
|
||||
\begin{itemize}
|
||||
\item $e$ is the current epoch, going from epoch $0$ to $e_c$, the current epoch
|
||||
\item $LFE(e)$ is the last finalized epoch before $e$
|
||||
\item $M$ is a very large constant
|
||||
\item $F$ is 1 if a safety failure has taken place, otherwise 0
|
||||
\end{itemize}
|
||||
|
||||
The second term in the function is easy to justify: safety failures are very bad. The first term is trickier. To see how the first term works, consider the case where every epoch such that $e$ mod $N$, for some $N$, is zero is finalized and other epochs are not. The average total over each $N$-epoch slice will be roughly $\sum_{i=1}^N -log_2(i) \approx N * (log_2(N) - \frac{1}{ln(2)})$. Hence, the utility per block will be roughly $-log_2(N)$. This basically states that a blockchain with some finality time $N$ has utility roughly $-log(N)$, or in other words \textit{increasing the finality time of a blockchain by a constant factor causes a constant loss of utility}. The utility difference between 1 minute finality and 2 minute finality is the same as the utility difference between 1 hour finality and 2 hour finality.
|
||||
|
||||
This can be justified in two ways. First, one can intuitively argue that a user's psychological estimation of the discomfort of waiting for finality roughly matches this kind of logarithmic utility schedule. At the very least, it should be clear that the difference between 3600 second finality and 3610 second finality feels much more negligible than the difference between 1 second finality and 11 second finality, and so the claim that the difference between 10 second finality and 20 second finality is similar to the difference between 1 hour finality and 2 hour finality should not seem farfetched. Second, one can look at various blockchain use cases, and see that they are roughly logarithmically uniformly distributed along the range of finality times between around 200 miliseconds (``Starcraft on the blockchain") and one week (land registries and the like).
|
||||
|
||||
Now, we need to show that, for any given total deposit size, $\frac{loss\_to\_protocol\_utility}{validator\_penalties}$ is bounded. There are two ways to reduce protocol utility: (i) cause a safety failure, and (ii) have $\ge \frac{1}{3}$ of validators not prepare or not commit to prevent finality. In the first case, validators lose a large amount of deposits for violating the slashing conditions. In the second case, in a chain that has not been finalized for $e - LFE$ epochs, the penalty to attackers is $$min(NPP * \frac{1}{3} + NPCP(\frac{1}{3}), NCP * \frac{1}{3} + NCCP(\frac{1}{3})) * BP(D, e, LFE)$$
|
||||
|
||||
To enforce a ratio between validator losses and loss to protocol utility, we set:
|
||||
|
||||
$$BP(D, e, LFE) = \frac{k}{D^p} + k_2 * floor(log_2(e - LFE))$$
|
||||
|
||||
The first term serves to take profits for non-committers away; the second term creates a penalty which is proportional to the loss in protocol utility.
|
||||
|
||||
This connection between validator losses and loss to protocol utility has several consequences. First, it establishes that harming the protocolexecution is costly, and harming the protocol execution more costs more. Second, it establishes that the protocol approximates the properties of a \textit{potential game} [cite]. Potential games have the property that Nash equilibria of the game correspond to local maxima of the potential function (in this case, protocol utility), and so correctly following the protocol is a Nash equilibrium even in cases where a coalition has more than $\frac{1}{3}$ of the total validators. Here, the protocol utility function is not a perfect potential function, as it does not always take into account changes in the \textit{quantity} of prepares and commits whereas validator rewards do, but it does come close.
|
||||
|
||||
\section{Griefing factor analysis}
|
||||
|
||||
Griefing factor analysis is important because it provides one way to quanitfy the risk to honest validators. In general, if all validators are honest, and if network latency stays below the length of an epoch, then validators face zero risk beyond the usual risks of losing or accidentally divulging access to their private keys. In the case where malicious validators exist, however, they can interfere in the protocol in ways that cause harm to both themselves and honest validators.
|
||||
|
||||
We can approximately define the "griefing factor" as follows:
|
||||
|
||||
\begin{definition}
|
||||
A strategy used by a coalition in a given mechanism exhibits a \textit{griefing factor} $B$ if it can be shown that this strategy imposes a loss of $B * x$ to those outside the coalition at the cost of a loss of $x$ to those inside the coalition. If all strategies that cause deviations from some given baseline state exhibit griefing factors less than or equal to some bound B, then we call B a \textit{griefing factor bound}.
|
||||
\end{definition}
|
||||
|
||||
A strategy that imposes a loss to outsiders either at no cost to a coalition, or to the benefit of a coalition, is said to have a griefing factor of infinity. Proof of work blockchains have a griefing factor bound of infinity because a 51\% coalition can double its revenue by refusing to include blocks from other participants and waiting for difficulty adjustment to reduce the difficulty. With selfish mining, the griefing factor may be infinity for coalitions of size as low as 23.21\%.
|
||||
|
||||
Let us start off our griefing analysis by not taking into account validator churn, so the validator set is always the same. In Casper, we can identify the following deviating strategies:
|
||||
|
||||
\begin{enumerate}
|
||||
\item A minority of validators do not prepare, or prepare incorrect values.
|
||||
\item (Mirror image of 1) A censorship attack where a majority of validators does not accept prepares from a minority of validators (or other isomorphic attacks such as waiting for the minority to prepare hash $H1$ and then preparing $H2$, making $H2$ the dominant chain and denying the victims their rewards)
|
||||
\item A minority of validators do not commit.
|
||||
\item (Mirror image of 3) A censorship attack where a majority of validators does not accept commits from a minority of validators
|
||||
\end{enumerate}
|
||||
|
||||
Notice that, from the point of view of griefing factor analysis, it is immaterial whether or not any hash in a given epoch was justified or finalized. The Casper mechanism only pays attention to finalization in order to calculate $BP(D, e, LFE)$, the penalty scaling factor. This value scales penalties evenly for all participants, so it does not affect griefing factors.
|
||||
|
||||
Let us now analyze the attack types:
|
||||
|
||||
\begin{tabularx}{\textwidth}{|X|X|X|}
|
||||
\hline
|
||||
Attack & Amount lost by attacker & Amount lost by victims \\
|
||||
\hline
|
||||
Minority of size $\alpha < \frac{1}{2}$ non-prepares & $NPP * \alpha + NPCP(\alpha) * \alpha$ & $NPCP(\alpha) * (1-\alpha)$ \\
|
||||
Majority censors $\alpha < \frac{1}{2}$ prepares & $NPCP(\alpha) * (1-\alpha)$ & $NPP * \alpha + NPCP(\alpha) * \alpha$ \\
|
||||
Minority of size $\alpha < \frac{1}{2}$ non-commits & $NCP * \alpha + NCCP(\alpha) * \alpha$ & $NCCP(\alpha) * (1-\alpha)$ \\
|
||||
Majority censors $\alpha < \frac{1}{2}$ commits & $NCCP(\alpha) * (1-\alpha)$ & $NCP * \alpha + NCCP(\alpha) * \alpha$ \\
|
||||
\hline
|
||||
\end{tabularx}
|
||||
|
||||
In general, we see a perfect symmetry between the non-commit case and the non-prepare case, so we can assume $\frac{NCCP(\alpha)}{NCP} = \frac{NPCP(\alpha)}{NPP}$. Also, from a protocol utility standpoint, we can make the observation that seeing $\frac{1}{3} \le p_c < \frac{2}{3}$ commits is better than seeing fewer commits, as it gives at least some economic security against finality reversions, so we do want to reward this scenario more than the scenario where we get $\frac{1}{3} \le p_c < \frac{2}{3}$ prepares. Another way to view the situation is to observe that $\frac{1}{3}$ non-prepares causes \textit{everyone} to non-commit, so it should be treated with equal severity.
|
||||
|
||||
In the normal case, anything less than $\frac{1}{3}$ commits provides no economic security, so we can treat $p_c < \frac{1}{3}$ commits as equivalent to no commits; this thus suggests $NPP = 2 * NCP$. We can also normalize $NCP = 1$.
|
||||
|
||||
Now, let us analyze the griefing factors, to try to determine an optimal shape for $NCCP$. The griefing factor for non-committing is:
|
||||
|
||||
$$\frac{(1-\alpha) * NCCP(\alpha)}{\alpha * (1 + NCCP(\alpha))}$$
|
||||
|
||||
The griefing factor for censoring is the inverse of this. If we want the griefing factor for non-committing to equal one, then we could compute:
|
||||
|
||||
$$\alpha * (1 + NCCP(\alpha)) = (1-\alpha) * NCCP(\alpha)$$
|
||||
|
||||
$$\frac{1 + NCCP(\alpha)}{NCCP(\alpha)} = \frac{1-\alpha}{\alpha}$$
|
||||
|
||||
$$\frac{1}{NCCP(\alpha)} = \frac{1-\alpha}{\alpha} - 1$$
|
||||
|
||||
$$NCCP(\alpha) = \frac{\alpha}{1-2\alpha}$$
|
||||
|
||||
Note that for $\alpha = \frac{1}{2}$, this would set the $NCCP$ to infinity. Hence, with this design a griefing factor of $1$ is infeasible. We \textit{can} achieve that effect in a different way - by making $NCP$ itself a function of $\alpha$; in this case, $NCCP = 1$ and $NCP = max(0, 1 - 2 * \alpha)$ would achieve the desired effect. If we want to keep the formula for $NCP$ constant, and the formula for $NCCP$ reasonably simple and bounded, then one alternative is to set $NCCP(\alpha) = \frac{\alpha}{1-\alpha}$; this keeps griefing factors bounded between $\frac{1}{2}$ and $2$.
|
||||
|
||||
\section{Pools}
|
||||
|
||||
In a traditional (ie. not sharded or otherwise scalable) blockchain, there is a limit to the number of validators that can be supported, because each validator imposes a substantial amount of overhead on the system. If we accept a maximum overhead of two consensus messages per second, and an epoch time of 1400 seconds, then this means that the system can handle 1400 validators (not 2800 because we need to count prepares and commits). Given that the number of individual users interested in staking will likely exceed 1400, this necessarily means that most users will participate through some kind of ``stake pool''.
|
||||
|
||||
Two other reasons to participate in stake pools are (i) to mitigate \textit{key theft risk} (i.e. an attacker hacking into their online machine and stealing the key), and (ii) to mitigate \textit{liveness risk}, the possibility that the validator node will go offline, perhaps because the operator does not have the time to manage a high-uptime setup.
|
||||
|
||||
There are several possible kinds of stake pools:
|
||||
|
||||
\begin{itemize}
|
||||
\item \textbf{Fully centrally managed}: users $B_1 ... B_n$ send coins to pool operator $A$. $A$ makes a few deposit transactions containing their combined balances, fully controls the prepare and commit process, and occasionally withdraws one of their deposits to accommodate users wishing to withdraw their balances. Requires complete trust.
|
||||
\item \textbf{Centrally managed but trust-reduced}: users $B_1 ... B_n$ send coins to a pool contract. The contract sends a few deposit transactions containing their combined balances, assigning pool operator $A$ control over the prepare and commit process, and the task of keeping track of withdrawal requests. $A$ occasionally withdraws one of their deposits to accommodate users wishing to withdraw their balances; the withdrawals go directly into the contract, which ensures each user's right to withdraw a proportional share. Users need to trust the operator not to get their coins lose, but the operator cannot steal the coins. The trust requirement can be reduced further if the pool operator themselves contributes a large portion of the coins, as this will disincentivize them from staking maliciously.
|
||||
\item \textbf{2-of-3}: a user makes a deposit transaction and specifies as validation code a 2-of-3 multisig, consisting of (i) the user's online key, (ii) the pool operator's online key, and (iii) the user's offline backup key. The need for two keys to sign off on a prepare, commit or withdraw minimizes key theft risk, and a liveness failure on the pool side can be handled by the user sending their backup key to another pool.
|
||||
\item \textbf{Multisig managed}: users $B_1 ... B_n$ send coins to a pool contract that works in the exact same way as a centrally managed pool, except that a multisig of several semi-trusted parties needs to approve each prepare and commit message.
|
||||
\item \textbf{Collective}: users $B_1 ... B_n$ send coins to a pool contract that that works in the exact same way as a centrally managed poolg
|
||||
, except that a threshold signature of at least portion $p$ of the users themselves (say, $p = 0.6$) needs to approve each prepare and commit messagge.
|
||||
\end{itemize}
|
||||
|
||||
We expect pools of different types to emerge to accomodate smaller users. In the long term, techniques such as blockchain sharding will make it possible to increase the number of users that can participate as validators directly, and techniques that allow validators to temporarily ``log out'' of the validator set when they are offline can mitigate liveness risk.
|
||||
|
||||
\section{Conclusions}
|
||||
|
||||
The above analysis gives a parametrized scheme for incentivizing in Casper, and shows that it is a Nash equilibrium in an uncoordinated-choice model with a wide variety of settings. We then attempt to derive one possible set of specific values for the various parameters by starting from desired objectives, and choosing values that best meet the desired objectives. This analysis does not include non-economic attacks, as those are covered by other materials, and does not cover more advanced economic attacks, including extortion and discouragement attacks. We hope to see more research in these areas, as well as in the abstract theory of what considerations should be taken into account when designing reward and penalty schedules.
|
||||
|
||||
\section{References}
|
||||
\bibliographystyle{abbrv}
|
||||
\bibliography{main}
|
||||
Optimal selfish mining strategies in Bitcoin; Ayelet Sapirshtein, Yonatan Sompolinsky, and Aviv Zohar: https://arxiv.org/pdf/1507.06183.pdf
|
||||
|
||||
Potential games; Dov Monderer and Lloyd Shapley: http://econpapers.repec.org/article/eeegamebe/v_3a14_3ay_3a1996_3ai_3a1_3ap_3a124-143.htm
|
||||
|
||||
\end{document}
|
||||
|
|
@ -1,403 +0,0 @@
|
|||
<h3>Casper The Friendly Finality Gadget</h3>
|
||||
|
||||
<p>This document describes a candidate design for the first implementation of Casper proof of stake on Ethereum. The proposal aims to achieve the key goals of deposit-based proof of stake including highly secure finality and low-cost consensus, but do so in a way that can be applied with minimal disruption to existing chains, including the current Ethereum proof of work chain. We describe the workings of the algorithm, show safety and liveness in a partially-synchronous fault-tolerance-theoretic model, and then proceed to describe the various considerations involving game-theoretic incentives, as well as how the system can automatically recover from >1/3 of nodes dropping offline, and with the use of lightweight out-of-band coordination assumptions, recover from various forms of 51% attacks. We will describe the algorithm in stages with increasing complexity, in order to show the core ideas first, and then bring in features such as validator set rotation and economic incentivization.</p>
|
||||
|
||||
<h3>Background</h3>
|
||||
|
||||
<p>Proof of stake has for a long time been viewed as a highly promising, but controversial, alternative to proof of work as a way of securing cryptoeconomic public blockchain consensus. Whereas proof of work measures economic consensus by measuring the quantity of computational resources that have been expended to "back" a particular state and history, proof of stake in simplest form seeks to replace physical mining with CPUs, GPUs and ASICs with "virtual mining" [cite], where economic consensus is measured by the economic resources inside the system that are committing to a given state and history.</p>
|
||||
|
||||
<p>However, early versions of proof of stake suffer from a flaw that is often called "nothing at stake" [cite], which states that if one naively builds a proof of stake algorithm by simply copying the intuitions and algorithms from proof of work, then the result is an algorithm where, in the event of a disagreement between whether to choose chain A or chain B, it is in every rational participant's interest to choose both. Unlike proof of work, where resources <em>on the outside</em> can be applied to either chain A or chain B but not both, in naive proof of stake the very fact of a chain split means that there is also a temporary split of the ledger of on-chain economic resources, and so a validator can use their copy of the resources on chain A to back chain A and a copy of their resources on chain B to back chain B.</p>
|
||||
|
||||
<p>PoW
|
||||
<img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/powsec.png" width="400px"></img> <br />
|
||||
PoS
|
||||
<img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/possec.png" width="400px"></img> </p>
|
||||
|
||||
<p>Casper builds on a tradition that was started with the description of <a href="#">Slasher</a> in early 2014, which attempts to explicitly detect such "equivocation" (a common Byzantine-fault-tolerance-theoretic term for the act of sending two messages that contradict each other, in this case by simultaneously supporting two conflicting forks), and economically penalize validators that are caught engaging in such behavior in order to discourage it.</p>
|
||||
|
||||
<p><img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/slasher1sec.png" width="400px"></img> </p>
|
||||
|
||||
<p>This solves nothing at stake (at the cost of an extremely weak synchrony assumption ("weak subjectivity") that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.</p>
|
||||
|
||||
<p>This allows for the introduction of a notion of <em>economic finality</em>:</p>
|
||||
|
||||
<blockquote>
|
||||
<p>A block, state or any constraint on the set of admissible histories can be considered <em>finalized</em> if it can be shown that if any incompatible block, state or constraint is also finalized (eg. two different blocks at the same height) then there exists evidence that can be used to penalize the parties at fault by some amount $X. This value X is called the <em>cryptoeconomic security margin</em> of the finality mechanism.</p>
|
||||
</blockquote>
|
||||
|
||||
<p>However, such strict forms of penalty-based proof of stake run into another risk: the possibility of "getting stuck":</p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*ftuBRQnM8v1kC0Lnvsh3zQ.jpeg" alt="" title="" /></p>
|
||||
|
||||
<p>A poorly designed algorithm could lead to a situation where it is not possible for any new block to be finalized, without at least some participants taking some action that would lead them to incur the penalty. Making an algorithm that can provide genuine finality, and that also avoids the possibility of getting stuck under all but the most exceptional circumstances, is a difficult challenge - but one that maps very well to problems that have already been studied for a long time under the aegis of Byzantine fault tolerance theory.</p>
|
||||
|
||||
<p>Algorithms such as PBFT, Paxos and HoneyBadger BFT [cite * 3] all try to achieve a similar goal, of achieving "consensus" between some group of nodes (sometimes called "processes"). An early attempt at defining the problem was through the Byzantine general's problem, where a group of generals are trying to coordinate on a specific plan for how to attack a city, but some of the generals may be traitors. The two goals are:</p>
|
||||
|
||||
<p>A. All loyal generals decide upon the same plan of action.
|
||||
B. A small number of traitors cannot cause the loyal generals to adopt a bad plan. [cite Lamport 1982] </p>
|
||||
|
||||
<p>In a consensus algorithm implemented in real life, the "plan of action" to be decided on is that of which operations are to be processed in what order.</p>
|
||||
|
||||
<p>In our case, the goal is not just to have one round of consensus to agree on a single value, but rather have ongoing rounds of consensus on an ever-growing chain. In a blockchain, every block contains the hash of the previous block, and so it is inherently linked to a history containing ancestor blocks going all the way back to some "genesis block" that was agreed to as one of the parameters of the protocol. Coming to consensus on a block inherently involves coming to consensus on all of its ancestors. Hence, the consensus algorithm must avoid not just coming to consensus on two conflicting blocks during one period, but rather it must also avoid coming to consensus on a block when it has already come to consensus on a block that conflicts with one of the block's ancestors.</p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*ARu6mWJ2_oWXZR0UB13hkQ.jpeg" alt="" title="" /></p>
|
||||
|
||||
<p>We will start off by presenting "Minimal Slashing Conditions", a mechanism that has this property, and that can also arguably be used in other contexts as a simpler alternative to PBFT.</p>
|
||||
|
||||
<h3>Minimal Slashing Conditions</h3>
|
||||
|
||||
<p>This algorithm assumes the existence of an underlying <strong>proposal mechanism</strong>, which creates a chain of blocks which is constantly growing, and where given a set of blocks there is a way to deterministically calculate what is the "tip" of the chain. The chain may grow in a perfectly orderly fashion, with one block being added to the tip every few seconds, or it may sometimes have "forks" where a given parent block has two children and one of the two children is eventually abandoned, or in the worst case the chain may grow highly chaotically, with multiple long-running branches with the identity of the tip constantly switching from one chain to another.</p>
|
||||
|
||||
<p>The proposal mechanism working with a relatively high level of quality is not necessary for safety; provided more than 2/3 of nodes correctly follow the protocol conflicting checkpoints will not be finalized no matter how poorly the proposal mechanism behaves. However, if the proposal mechanism behaves very poorly, this may prevent liveness.</p>
|
||||
|
||||
<p>The proposal mechanism is deliberately kept abstract; this can be a dictator, it can be a round-robin scheme between the participants in the consensus, or, as in our case with hybrid Casper, it will be the original proof of work chain.</p>
|
||||
|
||||
<p>Every hundredth block in the chain is called a <strong>checkpoint</strong>, and the period between two checkpoints is called an <strong>epoch</strong>. We assume the existence of a set of <strong>validators</strong> V<sub>1</sub> ... V<sub>n</sub>, with sizes S(V<sub>1</sub>) ... S(V<sub>n</sub>); in hybrid proof of stake each of these validators must have put down a deposit, and the amount of ETH in that deposit becomes their size.</p>
|
||||
|
||||
<p>Validators have the ability to send two classes of messages:</p>
|
||||
|
||||
<pre><code>[PREPARE, epoch, hash, epoch_source, hash_source]
|
||||
[COMMIT, epoch, hash]
|
||||
</code></pre>
|
||||
|
||||
<p>The intention is that during epoch <code>n</code>, validators wait for the proposal mechanism to create a checkpoint during epoch <code>n</code> (say, with hash <code>H</code>), and then create a PREPARE message for epoch <code>n</code> and hash <code>H</code>. The <code>epoch_souce</code> and <code>hash_source</code> values should refer to the most recent (in terms of epoch number) checkpoint that they know about that has received prepares from a set of validators PREPSET where <code>sum_{v in PREPSET} S(V) >= sum_{v in ALL_VALIDATORS} S(V) * 2/3</code> (hereinafter, we will refer to a set which has this property as "at least two thirds of validators"; any reference to a fraction of the validator set should be read as being weighted by size). If/when at least two thirds of validators create a PREPARE for <code>n</code> and <code>H</code> with the same <code>epoch_source</code> and <code>hash_source</code>, validators should then send a message to COMMIT <code>n</code> and <code>H</code>. If two thirds of validators do this, the checkpoint is considered finalized.</p>
|
||||
|
||||
<p>Although we say that validators "should" follow the above set of rules, in many circumstances there is no way to enforce that they are in fact doing so. For example, consider a case where the proposal mechanism forks and creates two competing checkpoints at epoch <code>n</code>, C1 and C2. Suppose that a validator sees C1 five seconds before C2. According to the above rules, the validator <em>should</em> prepare on C1. However, if the validator prepares on C2, this cannot be detected, because for all we know the message containing C1 <em>could</em> have been delayed by six seconds en route to that validator's computer and so the validator could have seen C2 first.</p>
|
||||
|
||||
<p>However, what we <em>can</em> do is identify a few specific cases where there is clear evidence that a validator acted incorrectly, and in these cases penalize the validator heavily - in fact, we can even go so far as to take away their entire deposit.</p>
|
||||
|
||||
<p>We can do this by defining a set of "slashing conditions", where if any validator triggers one of the four conditions they will lose their entire deposit. The conditions are as follows:</p>
|
||||
|
||||
<p>[copy from medium post https://medium.com/@VitalikButerin/minimal-slashing-conditions-20f0b500fc6c, "The slashing conditions are:" up to but not including "With these four slashing conditions, it turns out that both accountable safety and plausible liveness hold."]</p>
|
||||
|
||||
<p>We would like to prove two properties about this mechanism:</p>
|
||||
|
||||
<ol>
|
||||
<li><strong>Accountable safety</strong> : if two conflicting hashes get finalized, then it must be provably true that at least 1/3 of validators violated some slashing condition.</li>
|
||||
<li><strong>Plausible liveness</strong>: unless at least 1/3 of validators violated some slashing condition, there must exist a set of messages that 2/3 of validators can send which finalize some new hash without violating some slashing condition.</li>
|
||||
</ol>
|
||||
|
||||
<p>Details of a machine-verifiable proof in Isabelle can be <a href="https://medium.com/@pirapira/formal-methods-on-some-pos-stuff-e309775c2ab8">found here</a>. A proof sketch is as follows:</p>
|
||||
|
||||
<p>Suppose that two conflicting hashes C1 and C2 get finalized. This means that in some epoch e1, C1 has 2/3 prepares and 2/3 commits, and in some epoch e2, C2 has 2/3 prepares and 2/3 commits (if either of those sets of 2/3 prepares were missing, 2/3 of validators would have violated <code>PREPARE_REQ</code>).. First, consider the easy case where e1 = e2. Then, 2/3 prepares on C1 and 2/3 prepares on C2 require 1/3 of validators to have violated <code>NO_DBL_PREPARE</code>.</p>
|
||||
|
||||
<p>Now, without loss of generality, consider the case where e2 > e1. By <code>PREPARE_REQ</code> the 2/3 prepares on C2 imply 2/3 prepares during some previous epoch e2' < e2. This in turn implies 2/3 prepares during some epoch e2'', and so forth until one of two terminating cases:</p>
|
||||
|
||||
<p>(i) e2* = e1. Here, we have 2/3 prepares on C1, and 2/3 prepares on some ancestor of C2 which is not C1, and so 1/3 get slashed by <code>NO_DBL_PREPARE</code> <br />
|
||||
(ii) e2* < e1. Here, we have 2/3 prepares with <code>epoch > e1</code> and <code>epoch_source < e1</code>, as well as 2/3 commits with <code>epoch = e1</code>. Hence, at least 1/3 of the preparers must have violated <code>PREPARE_COMMIT_CONSISTENCY</code> </p>
|
||||
|
||||
<p>Plausible liveness can be proven even more easily. Suppose that (i) P is the highest epoch where there are 2/3 prepares, and (ii) M is the highest epoch when any message has been sent. By (i) there were no honest commits with epoch above P, and so 2/3 of validators can safely prepare any value with epoch M+1, and epoch source P. They can then safely commit that value.</p>
|
||||
|
||||
<h3>Hybrid fork choice rule</h3>
|
||||
|
||||
<p>The mechanism described above ensures <em>plausible liveness</em>; however, it does not ensure <em>actual liveness</em> - that is, while the mechanism cannot get stuck in the strict sense, it could still enter a scenario where the proposal mechanism gets into a state where it never ends up creating a checkpoint that could get finalized.</p>
|
||||
|
||||
<p>Here is one possible example:</p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*IhXmzZG9toAs3oedZX0spg.jpeg" width="400px"></img></p>
|
||||
|
||||
<p>In this case, HASH1 or any descendant thereof cannot be finalized without slashing 1/6 of validators. However, miners on a proof of work chain would interpret HASH1 as the head and start mining descendants of it. In fact, when <em>any</em> checkpoint gets k > 1/3 commits, no conflicting checkpoint can get finalized without <code>k - 1/3</code> of validators getting slashed.</p>
|
||||
|
||||
<p>This necessitates modifying the fork choice rule used by participants in the underlying proposal mechanism (as well as users and validators): instead of blindly following a longest-chain rule, there needs to be an overriding rule that (i) finalized checkpoints are favored, and (ii) when there are no further finalized checkpoints, checkpoints with more (justified) commits are favored.</p>
|
||||
|
||||
<p>One complete description of such a rule would be:</p>
|
||||
|
||||
<ol>
|
||||
<li>Start with HEAD equal to the genesis of the chain.</li>
|
||||
<li>Select the descendant checkpoint of HEAD with the most commits (only checkpoints with 2/3 prepares are admissible)</li>
|
||||
<li>Repeat (2) until no descendant with commits exists.</li>
|
||||
<li>Choose the longest proof of work chain from there.</li>
|
||||
</ol>
|
||||
|
||||
<p>The commit-following part of this rule can be viewed in some ways as mirroring the "greegy heaviest observed subtree" (GHOST) rule that has been proposed for proof of work chains. The symmetry is this: in GHOST, a node starts with the head at the genesis, then begins to move forward down the chain, and if it encounters a block with multiple children then it chooses the child that has the larger quantity of work built on top of it (including the child block itself and its descendants). Here, we follow a similar approach, except we repeatedly seek the child that comes the closest to achieving finality. A checkpoint is implicitly finalized if any of its descendants are finalized, and so we need to look at descendants and not just direct children. Finalizing a checkpoint requires 2/3 commits within a single epoch, and so we do not try to sum up commits across epochs and instead simply take the maximum.</p>
|
||||
|
||||
<h3>Adding Dynamic Validator Sets</h3>
|
||||
|
||||
<p>The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave. This introduces two classes of considerations. First, all of the above math assumes that the validator set that prepares and commits any two given checkpoints is identical. If this is not the case, then there may be situations where two conflicting checkpoints get finalized, but no one can be slashed because they were finalized by two completely different validator sets. </p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*3YfbZO5xwAxt-DrUIo2CmA.jpeg" alt="" title="" /></p>
|
||||
|
||||
<p>Hence, we need to think carefully about how validator set transitions happen and how one validator set "passes the baton" to the next. One nautral possibility is to only change the validator set if an epoch was finalized. This resolves the problem in its simplest form, as it means that there is no way to skip to the next validator set without finalizing a block with the previous validator set first.</p>
|
||||
|
||||
<p>However, this is still not a complete solution because it fails to take into account that the fact of whether or not an epoch was finalized <em>is itself something we do not yet have consensus on</em>. Hence, there exists a possible failure mode where two children get made on top of the same parent, where from one child's view the parent was finalized and from the other child's view the parent was not finalized:</p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*LZg61-hOWkuYH1pcgO3gYQ.png" alt="" title="" /></p>
|
||||
|
||||
<p>There are three ways out. One is for nodes to wait for two rounds of "finality" before considering a block finalized; one cannot achieve finality for both children without the signatures of the second round on one side and the first round of the other side intersecting. A second is to limit the rate at which validators can be swapped in and out, ensuring fault tolerance still stays close to 1/3. A third is to require signatures from both 2/3 of the current validator set and 2/3 of the previous validator set in order to consider a set of prepares or commits sufficient.</p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*RlTtXf7ymF-qyBwmtAb3GA.jpeg" alt="" title="" /></p>
|
||||
|
||||
<p><img src="https://cdn-images-1.medium.com/max/800/1*O1Tj6HvCiavDdHPVGrLJKg.png" alt="" title="" /></p>
|
||||
|
||||
<p>We make one modification to the fork choice rule: instead of taking the descendant with the highest percentage of commits from "the" validator set, we take the descendant checkpoint where the <em>minimum</em> of (i) the percentage of that checkpoint's <em>current</em> validator set that committed, and (ii) the percentage of that checkpoint's <em>previous</em> validator set that committed, is maximized.</p>
|
||||
|
||||
<h3>Joining and Leaving</h3>
|
||||
|
||||
<p>Now, we need to establish what is the specific mechanism by which validators can join and leave. We start off with a simple one:</p>
|
||||
|
||||
<ul>
|
||||
<li>Validators apply to join the validator set by sending a transaction containing (i) the ETH they want to deposit, (ii) the "validation code" (a kind of generalized public key), and (iii) the return address that their deposit will be sent to when they withdraw.</li>
|
||||
<li>If this transaction gets included during dynasty N, then they become part of dynasty N + 2, as well as all future dynasties until they decide to log off.</li>
|
||||
<li>Validators can "log off" by sending a transaction to do so. If it is included during dynasty N, then they will be logged off starting from dynasty N + 2.</li>
|
||||
<li>If a validator has been logged off for the past consecutive four months, then the validator can send another transaction to withdraw their deposit to their return address.</li>
|
||||
</ul>
|
||||
|
||||
<p>The two-dynasty delay ensures that the joining transaction will be confirmed by the time dynasty N + 1 begins, and so any candidate blocks that initiates dynasty N + 2 is guaranteed to have the same validator set for dynasty N + 2.</p>
|
||||
|
||||
<p>Note that the possibility of validator sets changing, and validators withdrawing their deposits, opens up another risk: <strong>long-range attacks</strong>. If a client has been logged off for more than four months, then there is a risk that a malicious majority of former validators, who were active at the time the client was now online but are now no longer active, can finalize a chain conflicting with the main chain, send this chain to the client, and the client will accept it. This necessarily means that at least half of this malicious majority violated a slashing condition, and under normal circumstances it would mean that their deposits are fully lost. In this case, however, <em>the offending validators have already taken their money out</em>; hence, they cannot be penalized.</p>
|
||||
|
||||
<p>This problem is not fully resolvable, unless we are willing to adopt a system where validators can never recover their deposits. What we <em>can</em> do, however, is better understand the precise requirements that we are imposing on clients and the network. A message should be considered "cryptoeconomically meaningful" only if the message is signed by a validator whose deposit is still certainly in the main chain. The way we can test this is that the client can keep track of the time that they most recently received a each finalized checkpoint, and only accept a child checkpoint if this checkpoint is received less than four months after the predecessor. This implies that in order to remain synchronized with the chain, clients need to be logged on every four months, and assuming clients are online constantly it implies a network synchrony assumption: any message signed can reach any node within two months (half of four months, as if a client detects a validator violating a slashing condition, the message needs to be included into a block before that validator can withdraw in order to destroy theire deposit).</p>
|
||||
|
||||
<h3>Economic Fundamentals</h3>
|
||||
|
||||
<p>The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite http://nakamotoinstitute.org/static/docs/anonymous-byzantine-consensus.pdf] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.</p>
|
||||
|
||||
<h3>Protocol utility function</h3>
|
||||
|
||||
<p>We will start off by specifying a "protocol utility function", a function which can be computed on any chain and which outputs a value that represents the "quality" of the chain. A unit decrease in protocol utility should be understood to represent a unit decrease in user satisfaction; our main objective when designing the incentive mechanism is to align incentives to maximize expected protocol utility. The utility function has no role in the actual protocol; it is simply a philosophical tool that we can use to evaluate how "good" a particular protocol execution is.</p>
|
||||
|
||||
<p>We define protocol utility as follows:</p>
|
||||
|
||||
<pre><code>sum_{epoch i = 1 ... n} -ln(i - LFE(i)) + c[i] - M * SF[i]
|
||||
</code></pre>
|
||||
|
||||
<p>Where:</p>
|
||||
|
||||
<ul>
|
||||
<li>LFE(i) refers to the last epoch in the chain before block i that was finalized (in an optimally running chain, this is always i-1)</li>
|
||||
<li>SF[i] = 1 if a safety failure was detected in epoch i, as defined by 1/3 of validators getting slashed, otherwise 0</li>
|
||||
<li>c[i] is the portion of commits in epoch i</li>
|
||||
<li>M is a (very large) constant</li>
|
||||
</ul>
|
||||
|
||||
<p>Note that there is no single principled way to say what the protocol utility is; this is a question that ultimately rests on the values of the users of the system. However, we can defend the reasoning behind each component in the above formula.</p>
|
||||
|
||||
<p>The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait <code>k</code> epochs for their transaction to be finalized is logarithmic in <code>k</code>. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. The separate <code>c</code> term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.</p>
|
||||
|
||||
<h3>Incentives</h3>
|
||||
|
||||
<p>We define the full set of incentives that we assign to validators in any given epoch as follows.</p>
|
||||
|
||||
<p>From the point of view of the state in which the incentives are being calculated, let us assume:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>e</code> is the epoch number</li>
|
||||
<li><code>H</code> is the hash of the most recent checkpoint block</li>
|
||||
<li><code>H_s</code> is the most recent justified checkpoint (ie. checkpoint with prepares from two thirds of the previous and current validator sets) that the state knows about </li>
|
||||
<li><code>k</code> is a constant</li>
|
||||
<li><code>TD</code> is the total size of deposits</li>
|
||||
<li><code>LFE(e)</code> is the last finalized epoch</li>
|
||||
<li><code>D</code> is a given validator's deposit size</li>
|
||||
</ul>
|
||||
|
||||
<p>During any epoch, define <code>BASE_INTEREST = D * k / sqrt(TD)</code> and <code>PENALTY_FACTOR = D * k / sqrt(TD) * log(1 + e - LFE(e))</code>. Abbreviate:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>NCP</code> = non-commit penalty</li>
|
||||
<li><code>NFP</code> = non-finality penalty</li>
|
||||
<li><code>NPP</code> = non-prepare penalty</li>
|
||||
<li><code>NCCP</code> = per-non-commit collective penalty</li>
|
||||
<li><code>NPCP</code> = per-non-prepare collective penalty</li>
|
||||
</ul>
|
||||
|
||||
<p>Assume all references to the five above variables in the remaining section are actually referring to <code>NCP * PENALTY_FACTOR</code>, <code>NFP * PENALTY_FACTOR</code>, etc.</p>
|
||||
|
||||
<p>We define the penalties as follows:</p>
|
||||
|
||||
<ul>
|
||||
<li>If the epoch is not finalized, all validators pay <code>NFP</code></li>
|
||||
<li>All non-committing validators pay <code>NCP</code>. Waived if 2/3 prepares are not found (ie. validators cannot legally commit).</li>
|
||||
<li>All non-preparing validators pay <code>NPP</code></li>
|
||||
<li>Suppose <code>cp</code> is the minimal fraction of validators between the two validator sets that commits (eg. if 80% of the validators in the current dynasty commit and 68% of the validators in the previous dynasty do, <code>cp = 0.68</code>). All validators pay <code>NCCP * (1 - cp)</code>. Waived if 2/3 prepares are not found (ie. validators cannot legally commit).</li>
|
||||
<li>Suppose <code>pp</code> is the minimal fraction of validators between the two validator sets that prepares. All validators pay <code>NPCP * (1-pp)</code></li>
|
||||
<li>If a validator violates a slashing condition, they lose their entire deposit.</li>
|
||||
</ul>
|
||||
|
||||
<h4>Uncoordinated Choice</h4>
|
||||
|
||||
<p>In an uncoordinated choice model, we assume that there is a validator set V<sub>1</sub> ... V<sub>n</sub>, with deposit sizes |V<sub>1</sub>| ... |V<sub>n</sub>|, and each validator acts independently according to their own incentives. We assume |V<sub>i</sub>| < 1/3.</p>
|
||||
|
||||
<p>Suppose that there is a number of competing unfinalized forks F1, F2 .. Fn. The validator's only possible actions are to (i) prepare a single <code>F_i</code> (if they prepare they will be slashed), and (ii) commit one or more <code>F_i</code>. Let <code>P(F_i)</code> be the probability that the validator believes that a given fork will be finalized (whether in this epoch or indirectly in a future one) conditional on that validator preparing on that fork. Let:</p>
|
||||
|
||||
<ul>
|
||||
<li><code>L(e, F_i)</code> be the validator's private expectation of the number of epochs until a descendant of <code>F_i</code> gets prepares from two thirds of validators.</li>
|
||||
</ul>
|
||||
|
||||
<p>The validator's expected return from preparing <code>F_i</code> is clearly <code>P(F_i) * D * NPP</code>. The validator can hence maximize revenues by going for the <code>F_i</code> with maximum probability of being finalized. This creates incentives for convergence. The validator's incentive for committing is made up of two components: (i) the reward <code>P(F_i) * D * NCP</code>, and (ii) an implied penalty <code>sum_{F_j: F_1 ... F_n, F_j != F_i} P(F_j) * NPP * L(e, F_j)</code> because if the validator commits on a fork that does not get adopted then they will be unable to prepare until two thirds of other validators prepare some future value. <code>L(e, F_j) >= 1</code>, so we can lower-bound the penalty with <code>(1 - P(F_i)) * D * NPP</code>. This suggests that validators will not commit a value unless they are at least <code>NPP / (NPP + NCP)</code> sure that it will be finalized.</p>
|
||||
|
||||
<h4>Coordinated Choice</h4>
|
||||
|
||||
<p>Any coalition of size equal to or greater than 1/3 of the total validator set can cause a safety or liveness failure. If they cause a safety failure, then they can get caught via the slashing conditions, and lose an amount of money equal to their entire security deposits. The trickier case is liveness failures.</p>
|
||||
|
||||
<p>The cheapest liveness failure to cause is for 1/3 of validators to continue preparing, but stop committing. In this case, they can delay finality by <code>d</code> epochs at a cost of <code>1/3 * TD * k / sqrt(TD) * 1/2 * sum(i = 2 ... d+1: log(i))</code> ~= <code>k * sqrt(TD) / 6 * ((d + 1) * log(d + 1) - (d + 1))</code>.</p>
|
||||
|
||||
<h3>Griefing Factor Analysis</h3>
|
||||
|
||||
<p>Another important kind of analysis to make in public economic protocols is the risk to honest validators. In general, if all validators are honest, and if network latency stays below the length of an epoch, then validators face zero risk beyond the usual risks of losing or accidentally divulging access to their private keys. In the case where malicious validators exist, we can analyze the risk to honest validators through <em>griefing factor analysis</em>.</p>
|
||||
|
||||
<p>We can approximately define the "griefing factor" as follows:</p>
|
||||
|
||||
<blockquote>
|
||||
<p>A strategy used by a coalition in a given mechanism exhibits a griefing factor B if it can be shown that this strategy imposes a loss of B * x to those outside the coalition at the cost of a loss of x to those inside the coalition.</p>
|
||||
</blockquote>
|
||||
|
||||
<p>Further:</p>
|
||||
|
||||
<blockquote>
|
||||
<p>If all strategies that cause deviations from some given baseline state exhibit griefing factors <= some bound B, then we call B a griefing factor bound.</p>
|
||||
</blockquote>
|
||||
|
||||
<p>A strategy that imposes a loss to outsiders either at no cost to a coalition, or to the benefit of a coalition, is said to have a griefing factor of infinity.</p>
|
||||
|
||||
<p>Fact:</p>
|
||||
|
||||
<blockquote>
|
||||
<p>Proof of work blockchains have a griefing factor bound of infinity.</p>
|
||||
</blockquote>
|
||||
|
||||
<p>Proof:</p>
|
||||
|
||||
<p>51% coalitions can double their revenue by refusing to build on blocks from all other miners, reducing the revenue of outside miners to zero. Due to selfish mining, griefing factor bounds are also infinity in all models that allow coalitions of size greater than ~0.2321 [cite], and even without selfish mining a miner can grief simply by mining with more hardware than the quantity that would maximize their profits.</p>
|
||||
|
||||
<p>Let us start off our griefing analysis by not taking into account validator churn, so all dynasties are identical. Because the equations involved are fractions of linear equations, we know that small churn will only lead to small changes in the results. In Casper, we can identify the following deviating strategies:</p>
|
||||
|
||||
<ol>
|
||||
<li>Less than 1/3 of validators do not commit.</li>
|
||||
<li>(Mirror image of 1) A censorship attack where 2/3 of validators block commits from less than 1/3 of validators.</li>
|
||||
<li>Less than 1/3 of validators do not prepare.</li>
|
||||
<li>(Mirror image of 3) A censorship attack where 2/3 of validators block prepares from less than 1/3 of validators.</li>
|
||||
<li>More than 1/3 of validators do not commit.</li>
|
||||
<li>(Mirror image of 5) A censorship attack where between 1/3 and 1/2 are blocked from committing (cannot be more because in the >1/2 case, the chain committed to by censorship victims will be viewed as winning)</li>
|
||||
<li>More than 1/3 of validators do not prepare.</li>
|
||||
<li>(Mirror image of 7) A censorship attack where between 1/3 and 1/2 are blocked from preparing.</li>
|
||||
</ol>
|
||||
|
||||
<p>We will ignore (8), because we assume in our model that the underlying proposal mechanism (ie. proof of work) is majority-honest, and there is no way for validators to do this.</p>
|
||||
|
||||
<p>Let us now analyze the griefing factors:</p>
|
||||
|
||||
<table>
|
||||
<tr>
|
||||
<td> Attack </td> <td> Amount lost by attacker </td> <td> Amount lost by victims </td> <td> Griefing factor </td> <td> Notes </td>
|
||||
</tr>
|
||||
<tr>
|
||||
<td> k < 1/3 non-commit </td> <td> NCP * k + NCCP * k<sup>2</sup></td> <td> NCCP * k * (1-k) </td> <td> NCCP / NCP </td>
|
||||
<td> The griefing factor is maximized when k -> 0 </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> Censor k < 1/3 committers </td> <td> NCCP * k * (1-k) </td> <td> NCP * k + NCCP * k<sup>2</sup></td> <td> 1.5 * (NCP + NCCP / 3) / NCCP </td>
|
||||
<td> The griefing factor is maximized when k -> 1/3 </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> k < 1/3 non-prepare </td> <td> NPP * k + NCCP * k<sup>2</sup></td> <td> NPCP * k * (1-k) </td> <td> NPCP / NPP </td>
|
||||
<td> The griefing factor is maximized when k -> 0 </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> Censor k < 1/3 preparers </td> <td> NPCP * k * (1-k) </td> <td> NPP * k + NPCP * k<sup>2</sup> </td> <td> 1.5 * (NPP + NPCP / 3) / NPCP </td>
|
||||
<td> The griefing factor is maximized when k -> 1/3 </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> k > 1/3 non-commit </td> <td> NFP * k + NCP * k + NCCP * k<sup>2</sup></td> <td> NFP * (1-k) + NCCP * k * (1-k)</td> <td>2 * (NFP + NCCP / 3) / (NFP + NCP + NCCP / 3)</td>
|
||||
<td> The griefing factor is maximized when k = 1/3 </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> Censor k > 1/3 non-committers </td> <td> NFP * (1-k) + NCCP * k * (1-k) </td> <td> NFP * k + NCP * k + NCCP * k<sup>2</sup> </td> <td> max(1 + NCCP / (NFP + NCP + NCCP / 2), (NFP + NCP + NCCP / 3) / (NFP + NCCP / 3) / 2)</td>
|
||||
<td> The griefing factor is maximized at either k -> 1/2, or k -> 1/3. </td>
|
||||
</tr>
|
||||
|
||||
<tr>
|
||||
<td> k > 1/3 non-prepare </td> <td> NFP * k + NPP * k + NPCP * k<sup>2</sup></td> <td> NFP * (1-k) + NPCP * k * (1-k)</td> <td>2 * (NFP + NPCP / 3) / (NFP + NPP + NPCP / 3)</td>
|
||||
<td> The griefing factor is maximized when k = 1/3 </td>
|
||||
</tr>
|
||||
|
||||
</table>
|
||||
|
||||
<p>There seems to be a three-dimensional space of optimal solutions with griefing factor bound 1.5, with constaints NCCP = NCP * 1.5 and NPCP = NPP * 1.5. One solution is:</p>
|
||||
|
||||
<p>NCP = 1/2 <br />
|
||||
NCCP = 3/4 <br />
|
||||
NPP = 1/2 <br />
|
||||
NPCP = 3/4 <br />
|
||||
NFP = 1 </p>
|
||||
|
||||
<p>The griefing factors are: (3/2, 3/2, 3/2, 3/2, 10/7, 7/5, 10/7)</p>
|
||||
|
||||
<p>However, we may want to voluntarily accept higher griefing factors against dominant coalitions in exchange for lower griefing factors against smaller coalitions, the reasoning being that this makes it easier to escape dominant attacking coalitions via a user-activated soft fork (see next section). In this case, an alternative solution is:</p>
|
||||
|
||||
<p>NCP = 3/2
|
||||
NCCP = 3/2
|
||||
NPP = 3/2
|
||||
NPCP = 3/2
|
||||
NFP = 1 </p>
|
||||
|
||||
<p>With griefing factors (1, 2, 1, 2, 1, 19/13, 1), a bound of 1.</p>
|
||||
|
||||
<p>There are other solutions; for example, (3, 3, 3, 3, 1) is interesting because it reduces the griefing factors for 1/3 coalitions that prevent finality to 0.8, and (1, 1, 1, 1, 0) reduces the griefing factor for all <50% finality-preventing coalitions to 0.5, at the cost of allowing coalitions of size > 50% to censor at griefing factors between 5/3 and 2. More generally, if we allow censoring coalitions a griefing factor of k, we can reduce the griefing factor for minority coalitions to 3 / (2 * k - 1). </p>
|
||||
|
||||
<h3>Recovering from Coalition Attacks</h3>
|
||||
|
||||
<p>Suppose that there exists a coalition of size >= 1/3 (possibly even size >= 2/3) that engages in attacks of type (5), (6) or (7) above. This type of attack can be resolved in honest nodes' favor, but in many cases (especially those where the dishonest coalition is of size >= 1/2) this requires some out-of-band coordination between users, which can only partially be automated. This does require a synchrony assumption between validators and users, but one on the order of weeks (more precisely, the synchrony assumption must be on the same order as the amount of time that a >33% attack will take to resolve; resolution taking weeks is arguably acceptable because the prepetrators will lose a large portion of their deposits in this kind of attack).</p>
|
||||
|
||||
<p>Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the first.</p>
|
||||
|
||||
<p>The offline validator loses <code>(NCP + NCCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. Online validators lose <code>(NCCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. With the "griefing factor bound 2" settings of (1, 1, 1, 1, 0), this gives a loss (expressed as percentage of total deposit) of 1 + 1/3 for the offline validator and a loss of 1/3 for online validators, so the offline validator's balance drains four times as quickly. If the online validator's share is 40% (ie. offline validator has 0.4x, online validators have 0.6x), for example, then the blockchain will once again commit when the balances decrease to (offline 0.272, online 0.545), at which point online validators once again have more than two thirds.</p>
|
||||
|
||||
<p>Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future. Suppose that the validator set is split into groups A and B, where A finalizes C1 and B finalizes C2. At the time of C1, the size of A is 0.667x, and the size of B is 0.333x. At the time of C2, the size of A is reduced to 0.111x, and the size of B is reduced to 0.222x. Hence, A can finalize C1 and B can finalize C2 with no slashing conditions violated.</p>
|
||||
|
||||
<p><img src="http://vitalik.ca/files/CommitsSync.png" alt="" title="" /></p>
|
||||
|
||||
<p>The purpose of this attack would be to convince a node that has been offline between C1 and C2 that C2 is the correct chain, when in reality it is C1 that is the correct chain. B would lose a large portion of their deposits on the C2 chain, but the C2 chain has little economic value as it is only used for this one particular attempt to defraud a set of clients, and so the attacker would emerge unscathed on the C1 chain.</p>
|
||||
|
||||
<p>This can be resolved by strengthening the synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).</p>
|
||||
|
||||
<p>Here are the results for the formulas above; note that the delay until finality can easily be scaled proportionately by any value.</p>
|
||||
|
||||
<p><img src="http://vitalik.ca/files/diag1.png" alt="" title="" />
|
||||
<img src="http://vitalik.ca/files/diag2.png?1" alt="" title="" /></p>
|
||||
|
||||
<h3>Recovering from Majority Censorship Attacks</h3>
|
||||
|
||||
<p>Now, let us consider the attacks where the censoring coalition is >= 1/2. Then, minority validators will refuse to build on chains that are censoring them, and so they will coordinate on their own chain. The result will be exactly the same as the result above: a majority chain and a minority chain, where under the rules of the protocol the majority chain will be able to finalize first, and where on the majority chain the victims will lose money faster than the attackers and so the attackers will be even stronger.</p>
|
||||
|
||||
<p>The asymmetry can be broken because users can manually implement a "user activated soft fork" where they refuse to accept the majority (attacking) chain, and so they can simply wait until the minority chain sheds deposits to the point where a checkpoint can be finalized by the non-colluding nodes. This coordination can be partially automated, as online nodes will be able to detect censorship, but it's impossible to make the automation perfect (as a perfect solution would violate impossibility results in distributed consensus); hence, a preferred solution is for nodes to give an alert if they believe the majority chain is attacking, and give the user an option of whether to continue with the majority chain or fork to the minority chain.</p>
|
||||
|
||||
<h3>Dealing with Failures in Proof of Work</h3>
|
||||
|
||||
<p>In this kind of design, the underlying chain is still generated by proof of work. However, there is much less need to worry about 51% attacks on the proof of work for several reasons.</p>
|
||||
|
||||
<p>There are three kinds of 51% attacks in proof of work:</p>
|
||||
|
||||
<ul>
|
||||
<li><strong>After the fact finality reversion</strong> - make a chain longer than the existing main chain, reverting a large number of blocks at the end of the existing main chain that were thought to be finalized.</li>
|
||||
<li><strong>Equivocation</strong> - create two "main chains" A and B that both appear long enough to be the main chain; convince one actor that A is finalized and another actor that B is finalized.</li>
|
||||
<li><strong>Censorship</strong> - refuse to include blocks and transactions from other miners.</li>
|
||||
</ul>
|
||||
|
||||
<p>Finality reversion is impossible outright for miners to carry out, as finality is defined by the finality gadget and not proof of work; this immediately eliminates the worst kind of 51% attack. Equivocation can be used to prevent finality by repeatedly creating multiple chains with different checkpoints for each epoch, so that validators never manage to put two thirds of their prepares behind a single one. Censorship can be used to prevent validators from being rewarded, along with the first-order consenquences of making the chain unusable.</p>
|
||||
|
||||
<p>If worse comes to worst, equivocation can be dealt with manually by having validators come together over an out-of-band communication channel to coordinate on finalizing checkpoints until a hard fork to replace the proof of work can be conducted. However, there is also another more automatable approach: validators can start ignoring checkpoints unless their proof of work meets a higher difficulty threshold. Suppose that malicious miners have an n:1 advantage against honest miners, and malicious miners need to create c competing checkpoints to reliably prevent convergence (say, c = 3, as if c = 2 then one of the two may easily get two thirds prepares by random chance). This will eventually lead to the situation where the malicious miners will attempt to create c admissible checkpoints and publish them simultaneously, and ~1 - c/n of the time they will succeed, but the other c/n of the time an honest miner will create a single checkpoint first, and the consensus will move forward. </p>
|
||||
|
||||
<h3>Selective Censorship Attacks</h3>
|
||||
|
||||
<p>Another kind of attack is that where either (i) >=1/3 of validators or (ii) >=1/2 of miners <em>selectively censor</em>; for example, they might fully cooperate within the consensus protocol but refuse to include transactions that match some blacklist. This can be dealt with by giving validators and users a <em>subjective fork choice rule</em>: they assign lower scores to blocks that appear to be not including transactions that should be included, and if censorship looks unambiguous they simply reject such blocks entirely.</p>
|
||||
|
||||
<p>This then degrades into a few cases:</p>
|
||||
|
||||
<ol>
|
||||
<li>>=1/2 of miners selectively censor; >=2/3 of validators do not participate. Then, the validators will simply coordinate on finalizing the longest non-censoring chain.</li>
|
||||
<li>>=1/3 of validators only sign chains that are selectively censoring. Then, from the point of view of non-participating validators, those validators are offline, and so this situation collapses into the liveness attack described in a previous section.</li>
|
||||
<li>Validators wrongly believe that censorship is taking place, because a network synchrony assumption is violated. In this case, some validators end up refusing to prepare or commit checkpoints that they would otherwise be preparing or committing, and so fewer or no blocks finalize until the network synchrony assumption once again takes hold.</li>
|
||||
</ol>
|
||||
|
||||
<h3>Discouragement Attacks</h3>
|
||||
|
||||
<p>Perhaps the most difficult kind of attack to deal with in this algorithm is a "discouragement attack". This attack happens in two stages. First, an attacker engages in a medium-grade liveness degradation attack, with the main goal of reducing the rewards for honest validators to below zero, or at least to below their capital lockup costs. Then, the attacker engages in more serious attacks on liveness or safety against a much smaller pool of honest validators. A discouragement attack requires the attacker to have an amount of deposits equal to 1/3 of the original total deposit size, but allows them to trigger liveness and safety failures much more cheaply.</p>
|
||||
|
||||
<p>It is worth noting that proof of work is extremely vulnerable to discouragement attacks: assuming a competitive market where miners have low profits, a selfish mining attack can quickly force other miners offline, at which point the miner can engage in a 51% attack. Hence, even if our treatment of discouragement attacks is not fully satisfactory, it arguably still fares substantially better than other protocols.</p>
|
||||
|
||||
<p>Along with minimizing griefing factors, we can mitigate discouragement attacks using another strategy: those who are currently non-validators can coordinate on joining the validator set en masse, overwhelming the attacker to the point that their share of the total validator set is less than 1/3 and their griefing is no longer effective. We expect many to be willing to join altruistically, but we can also recycle a portion of penalties into future rewards, thereby temporarily increasing the incentive for new joiners.</p>
|
||||
|
|
@ -1,214 +0,0 @@
|
|||
### Casper The Friendly Finality Gadget
|
||||
|
||||
This document describes a candidate design for the first implementation of Casper proof of stake on Ethereum. The proposal aims to achieve the key goals of deposit-based proof of stake including highly secure finality and low-cost consensus, but do so in a way that can be applied with minimal disruption to existing chains, including the current Ethereum proof of work chain. We describe the workings of the algorithm, show safety and liveness in a partially-synchronous fault-tolerance-theoretic model, and then proceed to describe the various considerations involving game-theoretic incentives, as well as how the system can automatically recover from >1/3 of nodes dropping offline, and with the use of lightweight out-of-band coordination assumptions, recover from various forms of 51% attacks. We will describe the algorithm in stages with increasing complexity, in order to show the core ideas first, and then bring in features such as validator set rotation and economic incentivization.
|
||||
|
||||
### Background
|
||||
|
||||
Proof of stake has for a long time been viewed as a highly promising, but controversial, alternative to proof of work as a way of securing cryptoeconomic public blockchain consensus. Whereas proof of work measures economic consensus by measuring the quantity of computational resources that have been expended to "back" a particular state and history, proof of stake in simplest form seeks to replace physical mining with CPUs, GPUs and ASICs with "virtual mining" [cite], where economic consensus is measured by the economic resources inside the system that are committing to a given state and history.
|
||||
|
||||
However, early versions of proof of stake suffer from a flaw that is often called "nothing at stake" [cite], which states that if one naively builds a proof of stake algorithm by simply copying the intuitions and algorithms from proof of work, then the result is an algorithm where, in the event of a disagreement between whether to choose chain A or chain B, it is in every rational participant's interest to choose both. Unlike proof of work, where resources _on the outside_ can be applied to either chain A or chain B but not both, in naive proof of stake the very fact of a chain split means that there is also a temporary split of the ledger of on-chain economic resources, and so a validator can use their copy of the resources on chain A to back chain A and a copy of their resources on chain B to back chain B.
|
||||
|
||||
PoW
|
||||
<img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/powsec.png" width="400px"></img>
|
||||
PoS
|
||||
<img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/possec.png" width="400px"></img>
|
||||
|
||||
Casper builds on a tradition that was started with the description of [Slasher](#) in early 2014, which attempts to explicitly detect such "equivocation" (a common Byzantine-fault-tolerance-theoretic term for the act of sending two messages that contradict each other, in this case by simultaneously supporting two conflicting forks), and economically penalize validators that are caught engaging in such behavior in order to discourage it.
|
||||
|
||||
<img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/slasher1sec.png" width="400px"></img>
|
||||
|
||||
This solves nothing at stake (at the cost of an extremely weak synchrony assumption ("weak subjectivity") that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.
|
||||
|
||||
This allows for the introduction of a notion of _economic finality_:
|
||||
|
||||
> A block, state or any constraint on the set of admissible histories can be considered _finalized_ if it can be shown that if any incompatible block, state or constraint is also finalized (eg. two different blocks at the same height) then there exists evidence that can be used to penalize the parties at fault by some amount $X. This value X is called the _cryptoeconomic security margin_ of the finality mechanism.
|
||||
|
||||
However, such strict forms of penalty-based proof of stake run into another risk: the possibility of "getting stuck":
|
||||
|
||||
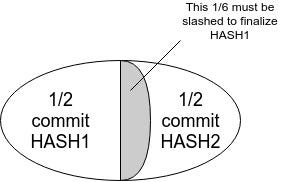
|
||||
|
||||
A poorly designed algorithm could lead to a situation where it is not possible for any new block to be finalized, without at least some participants taking some action that would lead them to incur the penalty. Making an algorithm that can provide genuine finality, and that also avoids the possibility of getting stuck under all but the most exceptional circumstances, is a difficult challenge - but one that maps very well to problems that have already been studied for a long time under the aegis of Byzantine fault tolerance theory.
|
||||
|
||||
Algorithms such as PBFT, Paxos and HoneyBadger BFT [cite * 3] all try to achieve a similar goal, of achieving "consensus" between some group of nodes (sometimes called "processes"). An early attempt at defining the problem was through the Byzantine general's problem, where a group of generals are trying to coordinate on a specific plan for how to attack a city, but some of the generals may be traitors. The two goals are:
|
||||
|
||||
A. All loyal generals decide upon the same plan of action.
|
||||
B. A small number of traitors cannot cause the loyal generals to adopt a bad plan. [cite Lamport 1982]
|
||||
|
||||
In a consensus algorithm implemented in real life, the "plan of action" to be decided on is that of which operations are to be processed in what order.
|
||||
|
||||
In our case, the goal is not just to have one round of consensus to agree on a single value, but rather have ongoing rounds of consensus on an ever-growing chain. In a blockchain, every block contains the hash of the previous block, and so it is inherently linked to a history containing ancestor blocks going all the way back to some "genesis block" that was agreed to as one of the parameters of the protocol. Coming to consensus on a block inherently involves coming to consensus on all of its ancestors. Hence, the consensus algorithm must avoid not just coming to consensus on two conflicting blocks during one period, but rather it must also avoid coming to consensus on a block when it has already come to consensus on a block that conflicts with one of the block's ancestors.
|
||||
|
||||
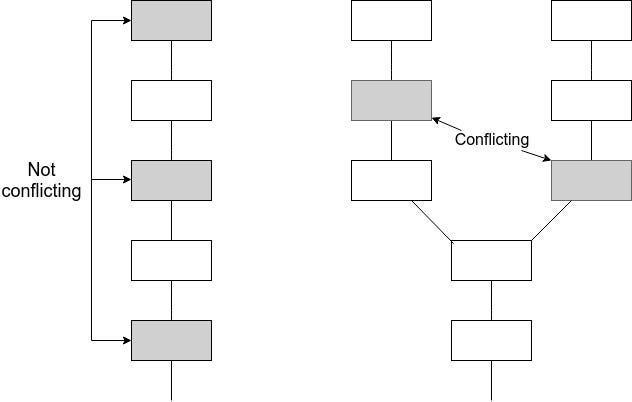
|
||||
|
||||
We will start off by presenting "Minimal Slashing Conditions", a mechanism that has this property, and that can also arguably be used in other contexts as a simpler alternative to PBFT.
|
||||
|
||||
### Minimal Slashing Conditions
|
||||
|
||||
This algorithm assumes the existence of an underlying **proposal mechanism**, which creates a chain of blocks which is constantly growing, and where given a set of blocks there is a way to deterministically calculate what is the "tip" of the chain. The chain may grow in a perfectly orderly fashion, with one block being added to the tip every few seconds, or it may sometimes have "forks" where a given parent block has two children and one of the two children is eventually abandoned, or in the worst case the chain may grow highly chaotically, with multiple long-running branches with the identity of the tip constantly switching from one chain to another.
|
||||
|
||||
The proposal mechanism working with a relatively high level of quality is not necessary for safety; provided more than 2/3 of nodes correctly follow the protocol conflicting checkpoints will not be finalized no matter how poorly the proposal mechanism behaves. However, if the proposal mechanism behaves very poorly, this may prevent liveness.
|
||||
|
||||
The proposal mechanism is deliberately kept abstract; this can be a dictator, it can be a round-robin scheme between the participants in the consensus, or, as in our case with hybrid Casper, it will be the original proof of work chain.
|
||||
|
||||
Every hundredth block in the chain is called a **checkpoint**, and the period between two checkpoints is called an **epoch**. We assume the existence of a set of **validators** V<sub>1</sub> ... V<sub>n</sub>, with sizes S(V<sub>1</sub>) ... S(V<sub>n</sub>); in hybrid proof of stake each of these validators must have put down a deposit, and the amount of ETH in that deposit becomes their size.
|
||||
|
||||
Validators have the ability to send two classes of messages:
|
||||
|
||||
[PREPARE, epoch, hash, epoch_source, hash_source]
|
||||
[COMMIT, epoch, hash]
|
||||
|
||||
The intention is that during epoch `n`, validators wait for the proposal mechanism to create a checkpoint during epoch `n` (say, with hash `H`), and then create a PREPARE message for epoch `n` and hash `H`. The `epoch_souce` and `hash_source` values should refer to the most recent (in terms of epoch number) checkpoint that they know about that has received prepares from a set of validators PREPSET where `sum_{v in PREPSET} S(V) >= sum_{v in ALL_VALIDATORS} S(V) * 2/3` (hereinafter, we will refer to a set which has this property as "at least two thirds of validators"; any reference to a fraction of the validator set should be read as being weighted by size). If/when at least two thirds of validators create a PREPARE for `n` and `H` with the same `epoch_source` and `hash_source`, validators should then send a message to COMMIT `n` and `H`. If two thirds of validators do this, the checkpoint is considered finalized.
|
||||
|
||||
Although we say that validators "should" follow the above set of rules, in many circumstances there is no way to enforce that they are in fact doing so. For example, consider a case where the proposal mechanism forks and creates two competing checkpoints at epoch `n`, C1 and C2. Suppose that a validator sees C1 five seconds before C2. According to the above rules, the validator _should_ prepare on C1. However, if the validator prepares on C2, this cannot be detected, because for all we know the message containing C1 _could_ have been delayed by six seconds en route to that validator's computer and so the validator could have seen C2 first.
|
||||
|
||||
However, what we _can_ do is identify a few specific cases where there is clear evidence that a validator acted incorrectly, and in these cases penalize the validator heavily - in fact, we can even go so far as to take away their entire deposit.
|
||||
|
||||
We can do this by defining a set of "slashing conditions", where if any validator triggers one of the four conditions they will lose their entire deposit. The conditions are as follows:
|
||||
|
||||
[copy from medium post https://medium.com/@VitalikButerin/minimal-slashing-conditions-20f0b500fc6c, "The slashing conditions are:" up to but not including "With these four slashing conditions, it turns out that both accountable safety and plausible liveness hold."]
|
||||
|
||||
We would like to prove two properties about this mechanism:
|
||||
|
||||
1. **Accountable safety** : if two conflicting hashes get finalized, then it must be provably true that at least 1/3 of validators violated some slashing condition.
|
||||
2. **Plausible liveness**: unless at least 1/3 of validators violated some slashing condition, there must exist a set of messages that 2/3 of validators can send which finalize some new hash without violating some slashing condition.
|
||||
|
||||
Details of a machine-verifiable proof in Isabelle can be [found here](https://medium.com/@pirapira/formal-methods-on-some-pos-stuff-e309775c2ab8). A proof sketch is as follows:
|
||||
|
||||
Suppose that two conflicting hashes C1 and C2 get finalized. This means that in some epoch e1, C1 has 2/3 prepares and 2/3 commits, and in some epoch e2, C2 has 2/3 prepares and 2/3 commits (if either of those sets of 2/3 prepares were missing, 2/3 of validators would have violated `PREPARE_REQ`).. First, consider the easy case where e1 = e2. Then, 2/3 prepares on C1 and 2/3 prepares on C2 require 1/3 of validators to have violated `NO_DBL_PREPARE`.
|
||||
|
||||
Now, without loss of generality, consider the case where e2 > e1. By `PREPARE_REQ` the 2/3 prepares on C2 imply 2/3 prepares during some previous epoch e2' < e2. This in turn implies 2/3 prepares during some epoch e2'', and so forth until one of two terminating cases:
|
||||
|
||||
(i) e2\* = e1. Here, we have 2/3 prepares on C1, and 2/3 prepares on some ancestor of C2 which is not C1, and so 1/3 get slashed by `NO_DBL_PREPARE`
|
||||
(ii) e2\* < e1. Here, we have 2/3 prepares with `epoch > e1` and `epoch_source < e1`, as well as 2/3 commits with `epoch = e1`. Hence, at least 1/3 of the preparers must have violated `PREPARE_COMMIT_CONSISTENCY`
|
||||
|
||||
Plausible liveness can be proven even more easily. Suppose that (i) P is the highest epoch where there are 2/3 prepares, and (ii) M is the highest epoch when any message has been sent. By (i) there were no honest commits with epoch above P, and so 2/3 of validators can safely prepare any value with epoch M+1, and epoch source P. They can then safely commit that value.
|
||||
|
||||
### Hybrid fork choice rule
|
||||
|
||||
The mechanism described above ensures _plausible liveness_; however, it does not ensure _actual liveness_ - that is, while the mechanism cannot get stuck in the strict sense, it could still enter a scenario where the proposal mechanism gets into a state where it never ends up creating a checkpoint that could get finalized.
|
||||
|
||||
Here is one possible example:
|
||||
|
||||
<img src="https://cdn-images-1.medium.com/max/800/1*IhXmzZG9toAs3oedZX0spg.jpeg" width="400px"></img>
|
||||
|
||||
In this case, HASH1 or any descendant thereof cannot be finalized without slashing 1/6 of validators. However, miners on a proof of work chain would interpret HASH1 as the head and start mining descendants of it. In fact, when *any* checkpoint gets k > 1/3 commits, no conflicting checkpoint can get finalized without `k - 1/3` of validators getting slashed.
|
||||
|
||||
This necessitates modifying the fork choice rule used by participants in the underlying proposal mechanism (as well as users and validators): instead of blindly following a longest-chain rule, there needs to be an overriding rule that (i) finalized checkpoints are favored, and (ii) when there are no further finalized checkpoints, checkpoints with more (justified) commits are favored.
|
||||
|
||||
One complete description of such a rule would be:
|
||||
|
||||
1. Start with HEAD equal to the genesis of the chain.
|
||||
2. Select the descendant checkpoint of HEAD with the most commits (only checkpoints with 2/3 prepares are admissible)
|
||||
3. Repeat (2) until no descendant with commits exists.
|
||||
4. Choose the longest proof of work chain from there.
|
||||
|
||||
The commit-following part of this rule can be viewed in some ways as mirroring the "greegy heaviest observed subtree" (GHOST) rule that has been proposed for proof of work chains. The symmetry is this: in GHOST, a node starts with the head at the genesis, then begins to move forward down the chain, and if it encounters a block with multiple children then it chooses the child that has the larger quantity of work built on top of it (including the child block itself and its descendants). Here, we follow a similar approach, except we repeatedly seek the child that comes the closest to achieving finality. A checkpoint is implicitly finalized if any of its descendants are finalized, and so we need to look at descendants and not just direct children. Finalizing a checkpoint requires 2/3 commits within a single epoch, and so we do not try to sum up commits across epochs and instead simply take the maximum.
|
||||
|
||||
### Adding Dynamic Validator Sets
|
||||
|
||||
The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave. This introduces two classes of considerations. First, all of the above math assumes that the validator set that prepares and commits any two given checkpoints is identical. If this is not the case, then there may be situations where two conflicting checkpoints get finalized, but no one can be slashed because they were finalized by two completely different validator sets.
|
||||
|
||||
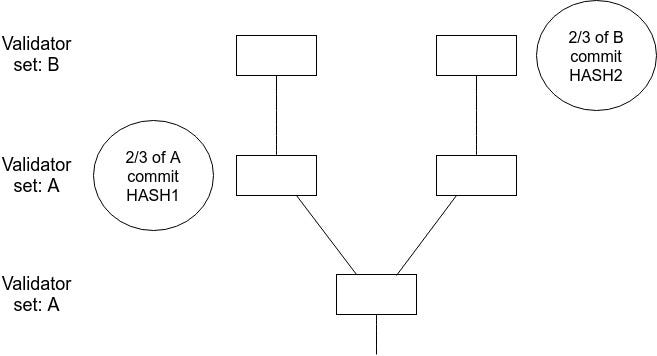
|
||||
|
||||
Hence, we need to think carefully about how validator set transitions happen and how one validator set "passes the baton" to the next. One nautral possibility is to only change the validator set if an epoch was finalized. This resolves the problem in its simplest form, as it means that there is no way to skip to the next validator set without finalizing a block with the previous validator set first.
|
||||
|
||||
However, this is still not a complete solution because it fails to take into account that the fact of whether or not an epoch was finalized _is itself something we do not yet have consensus on_. Hence, there exists a possible failure mode where two children get made on top of the same parent, where from one child's view the parent was finalized and from the other child's view the parent was not finalized:
|
||||
|
||||
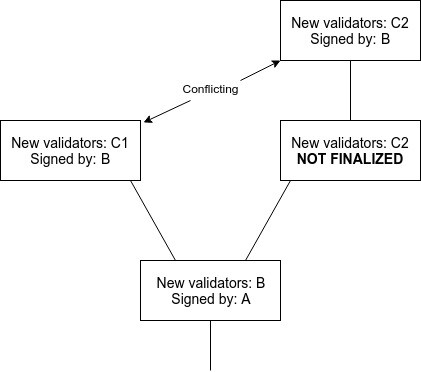
|
||||
|
||||
There are three ways out. One is for nodes to wait for two rounds of "finality" before considering a block finalized; one cannot achieve finality for both children without the signatures of the second round on one side and the first round of the other side intersecting. A second is to limit the rate at which validators can be swapped in and out, ensuring fault tolerance still stays close to 1/3. A third is to require signatures from both 2/3 of the current validator set and 2/3 of the previous validator set in order to consider a set of prepares or commits sufficient.
|
||||
|
||||
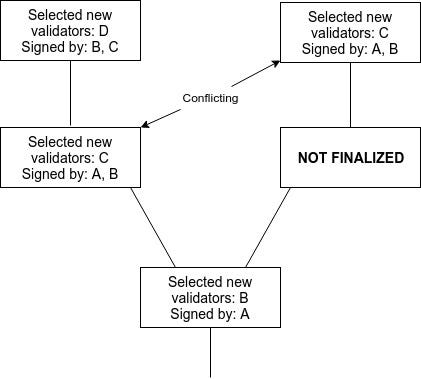
|
||||
|
||||
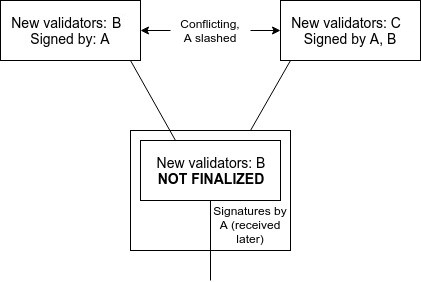
|
||||
|
||||
We make one modification to the fork choice rule: instead of taking the descendant with the highest percentage of commits from "the" validator set, we take the descendant checkpoint where the _minimum_ of (i) the percentage of that checkpoint's _current_ validator set that committed, and (ii) the percentage of that checkpoint's _previous_ validator set that committed, is maximized.
|
||||
|
||||
### Joining and Leaving
|
||||
|
||||
Now, we need to establish what is the specific mechanism by which validators can join and leave. We start off with a simple one:
|
||||
|
||||
* Validators apply to join the validator set by sending a transaction containing (i) the ETH they want to deposit, (ii) the "validation code" (a kind of generalized public key), and (iii) the return address that their deposit will be sent to when they withdraw.
|
||||
* If this transaction gets included during dynasty N, then they become part of dynasty N + 2, as well as all future dynasties until they decide to log off.
|
||||
* Validators can "log off" by sending a transaction to do so. If it is included during dynasty N, then they will be logged off starting from dynasty N + 2.
|
||||
* If a validator has been logged off for the past consecutive four months, then the validator can send another transaction to withdraw their deposit to their return address.
|
||||
|
||||
The two-dynasty delay ensures that the joining transaction will be confirmed by the time dynasty N + 1 begins, and so any candidate blocks that initiates dynasty N + 2 is guaranteed to have the same validator set for dynasty N + 2.
|
||||
|
||||
Note that the possibility of validator sets changing, and validators withdrawing their deposits, opens up another risk: **long-range attacks**. If a client has been logged off for more than four months, then there is a risk that a malicious majority of former validators, who were active at the time the client was now online but are now no longer active, can finalize a chain conflicting with the main chain, send this chain to the client, and the client will accept it. This necessarily means that at least half of this malicious majority violated a slashing condition, and under normal circumstances it would mean that their deposits are fully lost. In this case, however, _the offending validators have already taken their money out_; hence, they cannot be penalized.
|
||||
|
||||
This problem is not fully resolvable, unless we are willing to adopt a system where validators can never recover their deposits. What we _can_ do, however, is better understand the precise requirements that we are imposing on clients and the network. A message should be considered "cryptoeconomically meaningful" only if the message is signed by a validator whose deposit is still certainly in the main chain. The way we can test this is that the client can keep track of the time that they most recently received a each finalized checkpoint, and only accept a child checkpoint if this checkpoint is received less than four months after the predecessor. This implies that in order to remain synchronized with the chain, clients need to be logged on every four months, and assuming clients are online constantly it implies a network synchrony assumption: any message signed can reach any node within two months (half of four months, as if a client detects a validator violating a slashing condition, the message needs to be included into a block before that validator can withdraw in order to destroy theire deposit).
|
||||
|
||||
### Economic Fundamentals
|
||||
|
||||
The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite http://nakamotoinstitute.org/static/docs/anonymous-byzantine-consensus.pdf] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.
|
||||
|
||||
### Protocol utility function
|
||||
|
||||
We will start off by specifying a "protocol utility function", a function which can be computed on any chain and which outputs a value that represents the "quality" of the chain. A unit decrease in protocol utility should be understood to represent a unit decrease in user satisfaction; our main objective when designing the incentive mechanism is to align incentives to maximize expected protocol utility. The utility function has no role in the actual protocol; it is simply a philosophical tool that we can use to evaluate how "good" a particular protocol execution is.
|
||||
|
||||
We define protocol utility as follows:
|
||||
|
||||
sum_{epoch i = 1 ... n} -ln(i - LFE(i)) + c[i] - M * SF[i]
|
||||
|
||||
Where:
|
||||
|
||||
* LFE(i) refers to the last epoch in the chain before block i that was finalized (in an optimally running chain, this is always i-1)
|
||||
* SF[i] = 1 if a safety failure was detected in epoch i, as defined by 1/3 of validators getting slashed, otherwise 0
|
||||
* c[i] is the portion of commits in epoch i
|
||||
* M is a (very large) constant
|
||||
|
||||
Note that there is no single principled way to say what the protocol utility is; this is a question that ultimately rests on the values of the users of the system. However, we can defend the reasoning behind each component in the above formula.
|
||||
|
||||
The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait `k` epochs for their transaction to be finalized is logarithmic in `k`. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. The separate `c` term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.
|
||||
|
||||
### Recovering from Coalition Attacks
|
||||
|
||||
Suppose that there exists a coalition of size >= 1/3 (possibly even size >= 2/3) that engages in attacks of type (5), (6) or (7) above. This type of attack can be resolved in honest nodes' favor, but in many cases (especially those where the dishonest coalition is of size >= 1/2) this requires some out-of-band coordination between users, which can only partially be automated. This does require a synchrony assumption between validators and users, but one on the order of weeks (more precisely, the synchrony assumption must be on the same order as the amount of time that a >33% attack will take to resolve; resolution taking weeks is arguably acceptable because the prepetrators will lose a large portion of their deposits in this kind of attack).
|
||||
|
||||
Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the first.
|
||||
|
||||
The offline validator loses `(NCP + NCCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. Online validators lose `(NCCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. With the "griefing factor bound 2" settings of (1, 1, 1, 1, 0), this gives a loss (expressed as percentage of total deposit) of 1 + 1/3 for the offline validator and a loss of 1/3 for online validators, so the offline validator's balance drains four times as quickly. If the online validator's share is 40% (ie. offline validator has 0.4x, online validators have 0.6x), for example, then the blockchain will once again commit when the balances decrease to (offline 0.272, online 0.545), at which point online validators once again have more than two thirds.
|
||||
|
||||
Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future. Suppose that the validator set is split into groups A and B, where A finalizes C1 and B finalizes C2. At the time of C1, the size of A is 0.667x, and the size of B is 0.333x. At the time of C2, the size of A is reduced to 0.111x, and the size of B is reduced to 0.222x. Hence, A can finalize C1 and B can finalize C2 with no slashing conditions violated.
|
||||
|
||||

|
||||
|
||||
The purpose of this attack would be to convince a node that has been offline between C1 and C2 that C2 is the correct chain, when in reality it is C1 that is the correct chain. B would lose a large portion of their deposits on the C2 chain, but the C2 chain has little economic value as it is only used for this one particular attempt to defraud a set of clients, and so the attacker would emerge unscathed on the C1 chain.
|
||||
|
||||
This can be resolved by strengthening the synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).
|
||||
|
||||
Here are the results for the formulas above; note that the delay until finality can easily be scaled proportionately by any value.
|
||||
|
||||

|
||||

|
||||
|
||||
### Recovering from Majority Censorship Attacks
|
||||
|
||||
Now, let us consider the attacks where the censoring coalition is >= 1/2. Then, minority validators will refuse to build on chains that are censoring them, and so they will coordinate on their own chain. The result will be exactly the same as the result above: a majority chain and a minority chain, where under the rules of the protocol the majority chain will be able to finalize first, and where on the majority chain the victims will lose money faster than the attackers and so the attackers will be even stronger.
|
||||
|
||||
The asymmetry can be broken because users can manually implement a "user activated soft fork" where they refuse to accept the majority (attacking) chain, and so they can simply wait until the minority chain sheds deposits to the point where a checkpoint can be finalized by the non-colluding nodes. This coordination can be partially automated, as online nodes will be able to detect censorship, but it's impossible to make the automation perfect (as a perfect solution would violate impossibility results in distributed consensus); hence, a preferred solution is for nodes to give an alert if they believe the majority chain is attacking, and give the user an option of whether to continue with the majority chain or fork to the minority chain.
|
||||
|
||||
### Dealing with Failures in Proof of Work
|
||||
|
||||
In this kind of design, the underlying chain is still generated by proof of work. However, there is much less need to worry about 51% attacks on the proof of work for several reasons.
|
||||
|
||||
There are three kinds of 51% attacks in proof of work:
|
||||
|
||||
* **After the fact finality reversion** - make a chain longer than the existing main chain, reverting a large number of blocks at the end of the existing main chain that were thought to be finalized.
|
||||
* **Equivocation** - create two "main chains" A and B that both appear long enough to be the main chain; convince one actor that A is finalized and another actor that B is finalized.
|
||||
* **Censorship** - refuse to include blocks and transactions from other miners.
|
||||
|
||||
Finality reversion is impossible outright for miners to carry out, as finality is defined by the finality gadget and not proof of work; this immediately eliminates the worst kind of 51% attack. Equivocation can be used to prevent finality by repeatedly creating multiple chains with different checkpoints for each epoch, so that validators never manage to put two thirds of their prepares behind a single one. Censorship can be used to prevent validators from being rewarded, along with the first-order consenquences of making the chain unusable.
|
||||
|
||||
If worse comes to worst, equivocation can be dealt with manually by having validators come together over an out-of-band communication channel to coordinate on finalizing checkpoints until a hard fork to replace the proof of work can be conducted. However, there is also another more automatable approach: validators can start ignoring checkpoints unless their proof of work meets a higher difficulty threshold. Suppose that malicious miners have an n:1 advantage against honest miners, and malicious miners need to create c competing checkpoints to reliably prevent convergence (say, c = 3, as if c = 2 then one of the two may easily get two thirds prepares by random chance). This will eventually lead to the situation where the malicious miners will attempt to create c admissible checkpoints and publish them simultaneously, and ~1 - c/n of the time they will succeed, but the other c/n of the time an honest miner will create a single checkpoint first, and the consensus will move forward.
|
||||
|
||||
### Selective Censorship Attacks
|
||||
|
||||
Another kind of attack is that where either (i) >=1/3 of validators or (ii) >=1/2 of miners _selectively censor_; for example, they might fully cooperate within the consensus protocol but refuse to include transactions that match some blacklist. This can be dealt with by giving validators and users a _subjective fork choice rule_: they assign lower scores to blocks that appear to be not including transactions that should be included, and if censorship looks unambiguous they simply reject such blocks entirely.
|
||||
|
||||
This then degrades into a few cases:
|
||||
|
||||
1. >=1/2 of miners selectively censor; >=2/3 of validators do not participate. Then, the validators will simply coordinate on finalizing the longest non-censoring chain.
|
||||
2. >=1/3 of validators only sign chains that are selectively censoring. Then, from the point of view of non-participating validators, those validators are offline, and so this situation collapses into the liveness attack described in a previous section.
|
||||
3. Validators wrongly believe that censorship is taking place, because a network synchrony assumption is violated. In this case, some validators end up refusing to prepare or commit checkpoints that they would otherwise be preparing or committing, and so fewer or no blocks finalize until the network synchrony assumption once again takes hold.
|
||||
|
Before Width: | Height: | Size: 24 KiB |
|
Before Width: | Height: | Size: 22 KiB |
|
Before Width: | Height: | Size: 21 KiB |
|
Before Width: | Height: | Size: 20 KiB |
|
|
@ -1,90 +0,0 @@
|
|||
\usepackage{datetime}
|
||||
\title{A Note on Limits on Incentive Compatibility and Griefing Factors}
|
||||
\author{
|
||||
Vitalik Buterin \\
|
||||
Ethereum Foundation
|
||||
}
|
||||
\date{\today}
|
||||
\usepackage{graphicx}
|
||||
|
||||
\documentclass[12pt]{article}
|
||||
|
||||
\begin{document}
|
||||
\maketitle
|
||||
\begin{abstract}
|
||||
We show a fundamental tradeoff between extortion resistance and griefing resistance in the presence of non-uniquely-attributable faults: if extortion attacks in a consensus mechanism are unprofitable as long as portion $h$ of participants refuses to be extorted, then the mechanism has a griefing factor of at least $\frac{1}{2h} - 1$. We then discuss the notion of variable griefing factors, and propose a methodology for computing penalties for various participants given a particular honest (i.e. unextortable) minority assumption.
|
||||
\end{abstract}
|
||||
|
||||
\section{Introduction}
|
||||
Consider the general class of mechanisms where there exist an infinite set of infinitesimally small participants, and these participants have three strategies available: \textit{online}, \textit{offline} and \textit{censor}. Censoring participants choose as an argument the victims of the censorship. The mechanism has a partial view of what is going on: it can only see if participants are \textit{present} or \textit{absent}. It determines presence and absence as follows: there exists a set of size $\ge \frac{1}{2}$ of participants that is censoring the same participant set $P$, then any participant $p \in P$ is absent. A participant $p \not \in P$ (or, if no such $P$ exists, any participant $p$) is deemed present if they are online, and absent if they are offline. We deem this a reasonable approximation of consensus games, where being censored and being offline are, from the point of view of a majority chain, indistinguishable. The mechanism imposes some penalty to present validators and some penalty to absent validators (both penalties may depend on the total fraction of validators present).
|
||||
|
||||
We explore an "extortion attack", where an attacker (participant set $A$ of size $\ge \frac{1}{2}$) charges an extortion fee $f$, censoring all who do not pay up. Suppose $P_C$ is the mechanism-imposed penalty to a \textit{coalition member} (attacker or someone who pays the extortion fee), and $P_V$ is the prenalty to all others (\textit{victims}). Suppose portion $h$ of participants is "honest" (ie. unextortable). The cost paid by the attacker is $P_C * \frac{1}{2}$. The revenue from extortion is the size of the extorted size $\frac{1}{2} - h$ multiplied by the maximum possible extortion fee, $P_V - P_C$ (the difference between the loss of a victim and the loss of a coalition member; if the extortion fee was higher, it would not be rational to pay up).
|
||||
|
||||
\section{Analysis}
|
||||
|
||||
For extortion to be unprofitable, we must have:
|
||||
|
||||
$-\frac{1}{2} * P_C + (\frac{1}{2} - h) * (P_V - P_C) \le 0$
|
||||
|
||||
This can be rewritten:
|
||||
|
||||
$-\frac{1}{2} * P_C - (\frac{1}{2} - h) * P_C + (\frac{1}{2} - h) * P_V \le 0$
|
||||
|
||||
$(h - 1) * P_C \le (h - \frac{1}{2}) * P_V$
|
||||
|
||||
$\frac{P_C}{P_V} \ge \frac{\frac{1}{2} - h}{1 - h}$
|
||||
|
||||
Now, without loss of generality suppose $P_V = h - 1$ and $P_C = h - \frac{1}{2}$. We know from the above that the actual values are either these values or these values with two possible deviations: (i) scaling by some constant factor (ignorable because it does not change the griefing ratio) or (ii) setting $P_C$ \textit{higher} than the minimum (this increases the numerator of the below equation and hence makes the griefing factor even higher). Now, consider the scenario where fraction $h$ of participants are the attackers, and they attack by simply going offline. The griefing factor is total victim loss divided by total attacker loss, so it can be computed as:
|
||||
|
||||
$\frac{(1 - h) * (\frac{1}{2} - h)}{h * (1 - h)}$
|
||||
|
||||
$\frac{\frac{1}{2} - h}{h}$
|
||||
|
||||
$\frac{1}{2h} - 1$
|
||||
|
||||
If the honest minority assumption used is of size $\frac{1}{3}$, then the griefing factor must be at least $\frac{1}{2}$. If the honest minority assumption is of size $\frac{1}{4}$, then the griefing factor must be at least 1. If the honest minority assumption is of size $\frac{1}{8}$, then the griefing factor must be at least 3.
|
||||
|
||||
\section{Hugging the Wall}
|
||||
|
||||
One possible reaction to the above is as follows. The proof only shows that, if extortion is unprofitable with an honest minority of size $h$, then the griefing factor \textit{for a griefing attacker of size $h$} is $\frac{1}{2h} - 1$. Having high griefing factors \textit{in the specific case of small attackers} is not that bad, as the consequences are limited in size. So can we come up with a mechanism that "hugs the wall"; where the griefing factor is $\frac{1}{2}$ if the portion of absent participants is $\frac{1}{3}$, the griefing factor is 1 if the portion of absent participants is $\frac{1}{4}$, and so on?
|
||||
|
||||
We can show a relation for $P_C(\alpha)$ and $P_V(\alpha)$, where $\alpha$ is the portion of participants absent, that must hold for any hypothetical strategy that does hug the wall in terms of non-exploitability. We know:
|
||||
|
||||
$\frac{P_C(\alpha)}{P_V(\alpha)} \ge \frac{\alpha - \frac{1}{2}}{\alpha - 1}$
|
||||
|
||||
This is the same formula as one we saw above, but rewritten to make more explicit that $P_C$ and $P_V$ can both depend on $\alpha$. Let us rewrite this in the form of $P_C$, a penalty that everyone pays, and $P_A$, an extra penalty paid by absent participants, so $P_V = P_C + P_A$. We have:
|
||||
|
||||
$1 + \frac{P_A(\alpha)}{P_C(\alpha)} \le \frac{\alpha - 1}{\alpha - \frac{1}{2}}$
|
||||
|
||||
$1 + \frac{P_A(\alpha)}{P_C(\alpha)} \le 1 - \frac{\frac{1}{2}}{\alpha - \frac{1}{2}}$
|
||||
|
||||
$\frac{P_A(\alpha)}{P_C(\alpha)} \le \frac{1}{1 - 2\alpha}$
|
||||
|
||||
$P_A(\alpha) * (1 - 2\alpha) \le P_C(\alpha)$
|
||||
|
||||
We can achieve optimally low griefing factors if this holds with strict equality. We can also derive an optimal form for $P_C(\alpha)$. We know that we must have $P_C(0) = 0$ (if no participants are absent, no one should be punished, as that is the mechanism's "base case"). We want $P_C(\alpha)$ for $\alpha > 0$ to be positive to penalize censorship. To maximize penalties for any extortion attack where even one participant refuses to be extorted one could consider the formula:
|
||||
|
||||
\begin{array}
|
||||
$\alpha = 0$: $P(\alpha) = 0$ \\
|
||||
$\alpha > 0$: $P(\alpha) = 1$ \\
|
||||
\end{array}
|
||||
|
||||
However, this has the problem that if some portion of participants is \textit{naturally offline} (eg. because people's computers don't always work), then there is no longer any marginal censorship penalty. If we assume no knowledge about what portion of participants is likely to be naturally offline, then the most sensible formula for $P_C(\alpha)$ is that which maintains the same derivative everywhere so as to consistently punish censorship no matter what the quantity or starting conditions. Hence, we have $P_C(\alpha) = k * \alpha$.
|
||||
|
||||
From the above formula, we can then derive $P_A = k * \frac{\alpha}{1 - 2\alpha}$. One can check that these rules "hug the wall" perfectly: if an attacker has portion $\alpha$ of participants, and takes them all offline, then the griefing factor is $\frac{1}{2\alpha} - 1$, and an extortion attack in the best case leads to exactly zero revenue (in practice it will be costly because the attacker won't be able to capture literally 100\% of $P_A$ from extortion fees). If we are willing to accept higher griefing factors in exchange for making extortion attacks even more costly, a simple way to do this is to increase $P_C$ relative to $P_A$.
|
||||
|
||||
\includegraphics{chart1.png}
|
||||
\includegraphics{chart2.png}
|
||||
\includegraphics{chart3.png}
|
||||
|
||||
The formulas as given are likely not a good idea, as a griefing factor below $\frac{1}{2}$ for participants going offline implies a griefing factor greater than 2 for large-scale censorship. Hence, adding a "floor" at $\frac{1}{2}$ may be optimal. Additionally, if we are willing to accept an "honest majority" assumption of some $h$; that is, assume that fraction $h$ will never listen to an extortionist, then we can cap griefing factors even for small-scale griefing attacks. This can be accomplished by clamping $P_A$:
|
||||
|
||||
$P_A(\alpha) = clamp(h, \frac{\alpha}{1 - 2\alpha}, 1)$
|
||||
|
||||
\section{Conclusions}\label{conclusions}
|
||||
An honest minority model is a necessary part of a consensus mechanism's ability to resist extortion. The smaller the assumes honest minority, the higher the griefing factors that the protocol exposes itself to. However, if we are comfortable with accepting higher griefing factors for smaller attackers, then we can create penalty formulas that achieve closer-to-optimal results across a wide range of attacker sizes, although it becomes necessary for the penalty incurred by an absent participant for being absent to itself depend on the number of other absent participants.
|
||||
|
||||
\bibliographystyle{abbrv}
|
||||
\bibliography{main}
|
||||
|
||||
\end{document}
|
||||
|
Before Width: | Height: | Size: 44 KiB |
|
Before Width: | Height: | Size: 133 KiB |
|
Before Width: | Height: | Size: 29 KiB |
|
Before Width: | Height: | Size: 16 KiB After Width: | Height: | Size: 16 KiB |
|
Before Width: | Height: | Size: 4.5 KiB After Width: | Height: | Size: 4.5 KiB |
|
Before Width: | Height: | Size: 11 KiB After Width: | Height: | Size: 11 KiB |
|
Before Width: | Height: | Size: 13 KiB After Width: | Height: | Size: 13 KiB |
|
Before Width: | Height: | Size: 15 KiB After Width: | Height: | Size: 15 KiB |
|
Before Width: | Height: | Size: 26 KiB After Width: | Height: | Size: 26 KiB |
|
Before Width: | Height: | Size: 15 KiB After Width: | Height: | Size: 15 KiB |
|
Before Width: | Height: | Size: 15 KiB After Width: | Height: | Size: 15 KiB |
|
Before Width: | Height: | Size: 16 KiB After Width: | Height: | Size: 16 KiB |
|
Before Width: | Height: | Size: 15 KiB After Width: | Height: | Size: 15 KiB |
|
Before Width: | Height: | Size: 14 KiB After Width: | Height: | Size: 14 KiB |