Various edits

casper4/casper_paper.html

@@ -1,6 +1,6 @@
 <h3>Casper The Friendly Finality Gadget</h3>
 
-<p>This document describes a candidate design for the first implementation of Casper proof of stake on Ethereum. The proposal aims to achieve the key goals of deposit-based proof of stake including highly secure finality and low-cost consensus, but do so in a way that can be applied with minimal disruption to existing chains, including the current Ethereum proof of work chain. We describe the workings of the algorithm, show safety and liveness in a partially-synchronous fault-tolerance-theoretic model, and then proceed to describe the various considerations involving game-theoretic incentives. We will describe the algorithm in stages with increasing complexity, in order to show the core ideas first, and then bring in features such as validator set rotation and economic incentivization.</p>
+<p>This document describes a candidate design for the first implementation of Casper proof of stake on Ethereum. The proposal aims to achieve the key goals of deposit-based proof of stake including highly secure finality and low-cost consensus, but do so in a way that can be applied with minimal disruption to existing chains, including the current Ethereum proof of work chain. We describe the workings of the algorithm, show safety and liveness in a partially-synchronous fault-tolerance-theoretic model, and then proceed to describe the various considerations involving game-theoretic incentives, as well as how the system can automatically recover from >1/3 of nodes dropping offline, and with the use of lightweight out-of-band coordination assumptions, recover from various forms of 51% attacks. We will describe the algorithm in stages with increasing complexity, in order to show the core ideas first, and then bring in features such as validator set rotation and economic incentivization.</p>
 
 <h3>Background</h3>
 
@@ -17,7 +17,7 @@ PoS
 
 <p><img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/slasher1sec.png" width="400px"></img>  </p>
 
-<p>This solves nothing at stake (at the cost of an extremely weak synchrony assumption that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.</p>
+<p>This solves nothing at stake (at the cost of an extremely weak synchrony assumption ("weak subjectivity") that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.</p>
 
 <p>This allows for the introduction of a notion of <em>economic finality</em>:</p>
 
@@ -68,7 +68,7 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 
 <p>We can do this by defining a set of "slashing conditions", where if any validator triggers one of the four conditions they will lose their entire deposit. The conditions are as follows:</p>
 
-<p>[copy from medium post]</p>
+<p>[copy from medium post https://medium.com/@VitalikButerin/minimal-slashing-conditions-20f0b500fc6c, "The slashing conditions are:" up to but not including "With these four slashing conditions, it turns out that both accountable safety and plausible liveness hold."]</p>
 
 <p>We would like to prove two properties about this mechanism:</p>
 
@@ -113,11 +113,44 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 
 <h3>Adding Dynamic Validator Sets</h3>
 
-<p>The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave.</p>
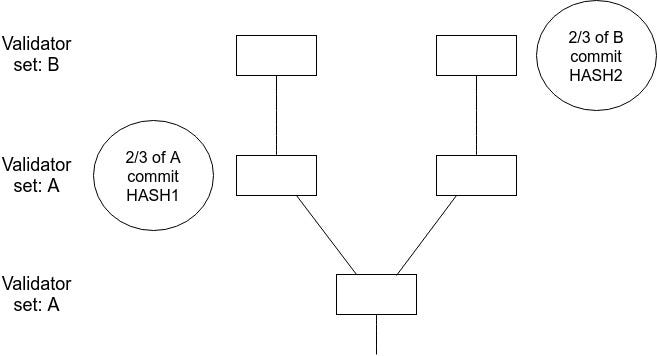
+<p>The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave. This introduces two classes of considerations. First, all of the above math assumes that the validator set that prepares and commits any two given checkpoints is identical. If this is not the case, then there may be situations where two conflicting checkpoints get finalized, but no one can be slashed because they were finalized by two completely different validator sets. </p>
+
+<p><img src="https://cdn-images-1.medium.com/max/800/1*3YfbZO5xwAxt-DrUIo2CmA.jpeg" alt="" title="" /></p>
+
+<p>Hence, we need to think carefully about how validator set transitions happen and how one validator set "passes the baton" to the next. One nautral possibility is to only change the validator set if an epoch was finalized. This resolves the problem in its simplest form, as it means that there is no way to skip to the next validator set without finalizing a block with the previous validator set first.</p>
+
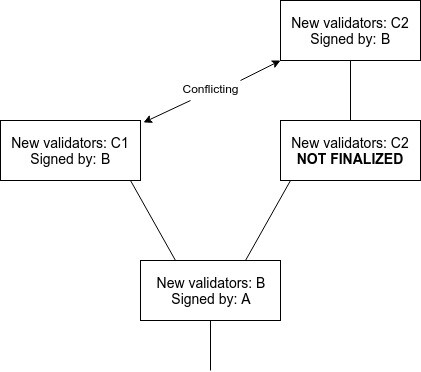
+<p>However, this is still not a complete solution because it fails to take into account that the fact of whether or not an epoch was finalized <em>is itself something we do not yet have consensus on</em>. Hence, there exists a possible failure mode where two children get made on top of the same parent, where from one child's view the parent was finalized and from the other child's view the parent was not finalized:</p>
+
+<p><img src="https://cdn-images-1.medium.com/max/800/1*LZg61-hOWkuYH1pcgO3gYQ.png" alt="" title="" /></p>
+
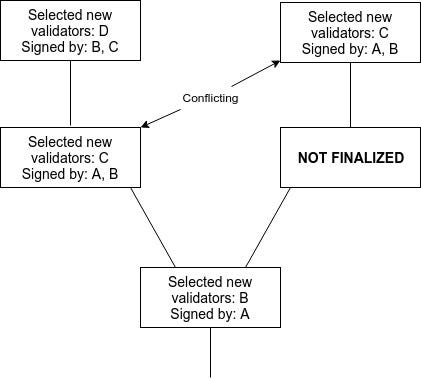
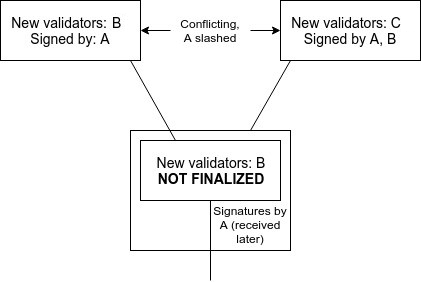
+<p>There are three ways out. One is for nodes to wait for two rounds of "finality" before considering a block finalized; one cannot achieve finality for both children without the signatures of the second round on one side and the first round of the other side intersecting. A second is to limit the rate at which validators can be swapped in and out, ensuring fault tolerance still stays close to 1/3. A third is to require signatures from both 2/3 of the current validator set and 2/3 of the previous validator set in order to consider a set of prepares or commits sufficient.</p>
+
+<p><img src="https://cdn-images-1.medium.com/max/800/1*RlTtXf7ymF-qyBwmtAb3GA.jpeg" alt="" title="" /></p>
+
+<p><img src="https://cdn-images-1.medium.com/max/800/1*O1Tj6HvCiavDdHPVGrLJKg.png" alt="" title="" /></p>
+
+<p>We make one modification to the fork choice rule: instead of taking the descendant with the highest percentage of commits from "the" validator set, we take the descendant checkpoint where the <em>minimum</em> of (i) the percentage of that checkpoint's <em>current</em> validator set that committed, and (ii) the percentage of that checkpoint's <em>previous</em> validator set that committed, is maximized.</p>
+
+<h3>Joining and Leaving</h3>
+
+<p>Now, we need to establish what is the specific mechanism by which validators can join and leave. We start off with a simple one:</p>
+
+<ul>
+<li>Validators apply to join the validator set by sending a transaction containing (i) the ETH they want to deposit, (ii) the "validation code" (a kind of generalized public key), and (iii) the return address that their deposit will be sent to when they withdraw.</li>
+<li>If this transaction gets included during dynasty N, then they become part of dynasty N + 2, as well as all future dynasties until they decide to log off.</li>
+<li>Validators can "log off" by sending a transaction to do so. If it is included during dynasty N, then they will be logged off starting from dynasty N + 2.</li>
+<li>If a validator has been logged off for the past consecutive four months, then the validator can send another transaction to withdraw their deposit to their return address.</li>
+</ul>
+
+<p>The two-dynasty delay ensures that the joining transaction will be confirmed by the time dynasty N + 1 begins, and so any candidate blocks that initiates dynasty N + 2 is guaranteed to have the same validator set for dynasty N + 2.</p>
+
+<p>Note that the possibility of validator sets changing, and validators withdrawing their deposits, opens up another risk: <strong>long-range attacks</strong>. If a client has been logged off for more than four months, then there is a risk that a malicious majority of former validators, who were active at the time the client was now online but are now no longer active, can finalize a chain conflicting with the main chain, send this chain to the client, and the client will accept it. This necessarily means that at least half of this malicious majority violated a slashing condition, and under normal circumstances it would mean that their deposits are fully lost. In this case, however, <em>the offending validators have already taken their money out</em>; hence, they cannot be penalized.</p>
+
+<p>This problem is not fully resolvable, unless we are willing to adopt a system where validators can never recover their deposits. What we <em>can</em> do, however, is better understand the precise requirements that we are imposing on clients and the network. A message should be considered "cryptoeconomically meaningful" only if the message is signed by a validator whose deposit is still certainly in the main chain. The way we can test this is that the client can keep track of the time that they most recently received a each finalized checkpoint, and only accept a child checkpoint if this checkpoint is received less than four months after the predecessor. This implies that in order to remain synchronized with the chain, clients need to be logged on every four months, and assuming clients are online constantly it implies a network synchrony assumption: any message signed can reach any node within two months (half of four months, as if a client detects a validator violating a slashing condition, the message needs to be included into a block before that validator can withdraw in order to destroy theire deposit).</p>
 
 <h3>Economic Fundamentals</h3>
 
-<p>The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.</p>
+<p>The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite http://nakamotoinstitute.org/static/docs/anonymous-byzantine-consensus.pdf] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.</p>
 
 <h3>Protocol utility function</h3>
 
@@ -139,7 +172,9 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 
 <p>Note that there is no single principled way to say what the protocol utility is; this is a question that ultimately rests on the values of the users of the system. However, we can defend the reasoning behind each component in the above formula.</p>
 
-<p>The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait <code>k</code> epochs for their transaction to be finalized is logarithmic in <code>k</code>. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. Another approach is to look at the possible set of blockchain applications, ranging from running games on them at the 100-1000 millisecond level, to retail payments at the 1-10 second level, other kinds of payments that currently take 1-10 minutes, and large institutional settlements that can take days, and see that they are roughly logarithmically distributed on the scale of the longest confirmation time that they could reasonably accept. The separate <code>c</code> term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.</p>
+<p>The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait <code>k</code> epochs for their transaction to be finalized is logarithmic in <code>k</code>. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. The separate <code>c</code> term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.</p>
+
+<p>The purpose of this function is to motivate the incentive structure, and show how large losses in protocol utility lead to proportionately large penalties for the perpetrator.</p>
 
 <h3>Incentives</h3>
 
@@ -173,10 +208,11 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 
 <ul>
 <li>If the epoch is not finalized, all validators pay <code>NFP</code></li>
-<li>All non-committing validators pay <code>NCP</code></li>
+<li>All non-committing validators pay <code>NCP</code>. Waived if 2/3 prepares are not found (ie. validators cannot legally commit).</li>
 <li>All non-preparing validators pay <code>NPP</code></li>
-<li>Suppose <code>cp</code> is the minimal fraction of validators between the two validator sets that commits (eg. if 80% of the validators in the current dynasty commit and 68% of the validators in the previous dynasty do, <code>cp = 0.68</code>). All validators pay <code>NCCP * (1 - cp)</code>. Waived if 2/3 prepares are not found.</li>
+<li>Suppose <code>cp</code> is the minimal fraction of validators between the two validator sets that commits (eg. if 80% of the validators in the current dynasty commit and 68% of the validators in the previous dynasty do, <code>cp = 0.68</code>). All validators pay <code>NCCP * (1 - cp)</code>. Waived if 2/3 prepares are not found (ie. validators cannot legally commit).</li>
 <li>Suppose <code>pp</code> is the minimal fraction of validators between the two validator sets that prepares. All validators pay <code>NPCP * (1-pp)</code></li>
+<li>If a validator violates a slashing condition, they lose their entire deposit.</li>
 </ul>
 
 <h4>Uncoordinated Choice</h4>
@@ -272,12 +308,12 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 </tr>
 
 <tr>
-<td> Censor k > 1/3 non-committers </td> <td> NFP * (1-k) + NCCP * k * (1-k) </td> <td> NFP * k + NCP * k + NCCP * k<sup>2</sup> </td> <td> 1 + NCCP / (NFP + NCP + NCCP / 2)</td>
-<td> The griefing factor is maximized when k -> 1/2 </td>
+<td> Censor k > 1/3 non-committers </td> <td> NFP * (1-k) + NCCP * k * (1-k) </td> <td> NFP * k + NCP * k + NCCP * k<sup>2</sup> </td> <td> max(1 + NCCP / (NFP + NCP + NCCP / 2), (NFP + NCP + NCCP / 3) / (NFP + NCCP / 3) / 2)</td>
+<td> The griefing factor is maximized at either k -> 1/2, or k -> 1/3. </td>
 </tr>
 
 <tr>
-<td> k > 1/3 non-prepare </td> <td> NFP * k + NCP * k + NPP * k + NPCP * k<sup>2</sup></td> <td> NFP * (1-k) + NCP * (1-k) + NPCP * k * (1-k)</td> <td>2 * (NFP + NCP + NPCP / 3) / (NFP + NCP + NPP + NPCP / 3)</td>
+<td> k > 1/3 non-prepare </td> <td> NFP * k + NPP * k + NPCP * k<sup>2</sup></td> <td> NFP * (1-k) + NPCP * k * (1-k)</td> <td>2 * (NFP + NPCP / 3) / (NFP + NPP + NPCP / 3)</td>
 <td> The griefing factor is maximized when k = 1/3 </td>
 </tr>
 
@@ -287,49 +323,44 @@ B. A small number of traitors cannot cause the loyal generals to adopt a bad pla
 
 <p>NCP = 1/2 <br />
 NCCP = 3/4 <br />
-NPP = 2/3 <br />
-NPCP = 1 <br />
+NPP = 1/2 <br />
+NPCP = 3/4 <br />
 NFP = 1  </p>
 
-<p>The griefing factors are: (3/2, 3/2, 3/2, 3/2, 10/7, 7/5, 44/30)</p>
+<p>The griefing factors are: (3/2, 3/2, 3/2, 3/2, 10/7, 7/5, 10/7)</p>
 
 <p>However, we may want to voluntarily accept higher griefing factors against dominant coalitions in exchange for lower griefing factors against smaller coalitions, the reasoning being that this makes it easier to escape dominant attacking coalitions via a user-activated soft fork (see next section). In this case, an alternative solution is:</p>
 
-<p>NCP = 1.5 <br />
-NCCP = 1.5 <br />
-NPP = 3.75 <br />
-NPCP = 3.75 <br />
+<p>NCP = 3/2
+NCCP = 3/2
+NPP = 3/2
+NPCP = 3/2
 NFP = 1  </p>
 
 <p>With griefing factors (1, 2, 1, 2, 1, 19/13, 1), a bound of 1.</p>
 
-<p>Increasing the griefing factor bound for censoring coalitions to 3 introduces a solution:</p>
-
-<p>NCP = 5 <br />
-NCCP = 3 <br />
-NPP = 26.667 <br />
-NPCP = 16 <br />
-NFP = 1  </p>
-
-<p>With griefing factors (3/5, 3, 3/5, 3, 4/7, 7/5, 34/57), a bound of 3/5.</p>
-
-<p>And increasing to 3 introduces </p>
+<p>There are other solutions; for example, (3, 3, 3, 3, 1) is interesting because it reduces the griefing factors for 1/3 coalitions that prevent finality to 0.8, and (1, 1, 1, 1, 0) reduces the griefing factor for all &lt;50% finality-preventing coalitions to 0.5, at the cost of allowing coalitions of size > 50% to censor at griefing factors between 5/3 and 2. More generally, if we allow censoring coalitions a griefing factor of k, we can reduce the griefing factor for minority coalitions to 3 / (2 * k - 1). </p>
 
 <h3>Recovering from Coalition Attacks</h3>
 
 <p>Suppose that there exists a coalition of size >= 1/3 (possibly even size >= 2/3) that engages in attacks of type (5), (6) or (7) above. This type of attack can be resolved in honest nodes' favor, but in many cases (especially those where the dishonest coalition is of size >= 1/2) this requires some out-of-band coordination between users, which can only partially be automated. This does require a synchrony assumption between validators and users, but one on the order of weeks (more precisely, the synchrony assumption must be on the same order as the amount of time that a >33% attack will take to resolve; resolution taking weeks is arguably acceptable because the prepetrators will lose a large portion of their deposits in this kind of attack).</p>
 
-<p>Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the second.</p>
+<p>Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the first.</p>
 
-<p>The offline validator loses <code>(NCP + NPP + NPCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. Online validators lose <code>(NCP + NPCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. With the "griefing factor bound 2" settings, this gives a loss of 1.5 + 3.75 + 1.25 + 1 = 7.5 for the offline validator and a loss of 1.5 + 1.25 + 1 = 3.75 for online validators, so the offline validator's balance drains twice as quickly. Suppose that the original fraction of the offline validator is p > 1/3, and let t be the fraction of each online validator's balance remaining. Users need to wait until the balances decrease, to the point where <code>p * t**2 = 1/2 * (1 - p) * t</code>, or <code>t = (1-p) / 2p</code>. For example, if 40% of validators drop offline, then <code>t = 0.75</code>, and so online validators will lose 25% of their funds and offline validators will lose 43.75%.</p>
+<p>The offline validator loses <code>(NCP + NCCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. Online validators lose <code>(NCCP * 1/3 + NFP) * PENALTY_FACTOR</code> times their balance. With the "griefing factor bound 2" settings of (1, 1, 1, 1, 0), this gives a loss (expressed as percentage of total deposit) of 1 + 1/3 for the offline validator and a loss of 1/3 for online validators, so the offline validator's balance drains four times as quickly. If the online validator's share is 40% (ie. offline validator has 0.4x, online validators have 0.6x), for example, then the blockchain will once again commit when the balances decrease to (offline 0.272, online 0.545), at which point online validators once again have more than two thirds.</p>
 
-<p>Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future, where <code>t = 1/2</code> (say, this is after three weeks). It's entirely possible for two thirds of the validator set in C1 to finalize C1, where the remaining one third is precisely the two thirds of the validator set in C2 that then finalizes C2.</p>
+<p>Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future. Suppose that the validator set is split into groups A and B, where A finalizes C1 and B finalizes C2. At the time of C1, the size of A is 0.667x, and the size of B is 0.333x. At the time of C2, the size of A is reduced to 0.111x, and the size of B is reduced to 0.222x. Hence, A can finalize C1 and B can finalize C2 with no slashing conditions violated.</p>
 
-<p>[diagram]</p>
+<p><img src="http://vitalik.ca/files/CommitsSync.png" alt="" title="" /></p>
 
-<p>This can be resolved with a synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).</p>
+<p>The purpose of this attack would be to convince a node that has been offline between C1 and C2 that C2 is the correct chain, when in reality it is C1 that is the correct chain. B would lose a large portion of their deposits on the C2 chain, but the C2 chain has little economic value as it is only used for this one particular attempt to defraud a set of clients, and so the attacker would emerge unscathed on the C1 chain.</p>
 
-<p>More formally, if C2 comes after C1, and the t values are t(C2) and t(C1), then the amount of equivocation required is <code>(2/3 * t(C2) + 2/3 * t(C1)) - t(C1)</code>, and inside of C1 <code>1 - t(C1)</code> would be lost due to the non-validation penalties - a total loss of <code>2/3 * t(C2) - 1/3 * t(C1) + 1 - t(C1)</code>, or <code>2/3 * t(C2) + 1 - 4/3 * t(C1)</code>. Regardless of <code>t(C2)</code>, this is clearly minimized when <code>t(C1) = 1</code>, so we have <code>2/3 * t(C2) - 1/3</code>. With the above synchrony assumption, we only need to be concerned about C2 if the distance is C1 and C2 is sufficiently small, and so we can specify a lower bound on <code>t(C2)</code>.</p>
+<p>This can be resolved by strengthening the synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).</p>
+
+<p>Here are the results for the formulas above; note that the delay until finality can easily be scaled proportionately by any value.</p>
+
+<p><img src="http://vitalik.ca/files/diag1.png" alt="" title="" />
+<img src="http://vitalik.ca/files/diag2.png" alt="" title="" /></p>
 
 <p>Now, let us consider the attacks where the censoring coalition is >= 1/2. Then, minority validators will refuse to build on chains that are censoring them, and so they will coordinate on their own chain. The result will be exactly the same as the result above: a majority chain and a minority chain, where under the rules of the protocol the majority chain will be able to finalize first, and where on the majority chain the victims will lose money faster than the attackers and so the attackers will be even stronger.</p>
 

casper4/casper_paper.md

@@ -17,7 +17,7 @@ Casper builds on a tradition that was started with the description of [Slasher](
 
 <img src="https://raw.githubusercontent.com/vbuterin/diagrams/master/slasher1sec.png" width="400px"></img>  
 
-This solves nothing at stake (at the cost of an extremely weak synchrony assumption that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.
+This solves nothing at stake (at the cost of an extremely weak synchrony assumption ("weak subjectivity") that will be discussed later), and ensures that such proof of stake algorithms can be at least as secure as proof of work. However, we can go further. It was soon discovered by Vlad Zamfir that consensus algorithms based on penalties could be made vastly more secure than consensus algorithms that are purely based on rewards, because there is an inherent asymmetry between the two. Whereas rewards are inherently limited in the size of the incentive that they offer, as every reward paid out must be paid out by the protocol, penalties can theoretically go much higher, potentially even all the way up to the entire pool of capital that the participant is participating in the proof of stake mechanism with.
 
 This allows for the introduction of a notion of _economic finality_:
 
@@ -65,7 +65,7 @@ However, what we _can_ do is identify a few specific cases where there is clear
 
 We can do this by defining a set of "slashing conditions", where if any validator triggers one of the four conditions they will lose their entire deposit. The conditions are as follows:
 
-[copy from medium post]
+[copy from medium post https://medium.com/@VitalikButerin/minimal-slashing-conditions-20f0b500fc6c, "The slashing conditions are:" up to but not including "With these four slashing conditions, it turns out that both accountable safety and plausible liveness hold."]
 
 We would like to prove two properties about this mechanism:
 
@@ -106,15 +106,42 @@ The commit-following part of this rule can be viewed in some ways as mirroring t
 
 ### Adding Dynamic Validator Sets
 
-The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave. This introduces two classes of considerations. First, all of the above math assumes that the validator set that prepares and commits any two given checkpoints is identical. If this is not the case, then there may be situations where two conflicting checkpoints get finalized, but no one can be slashed because they were finalized by two completely different validator sets. Hence, we need to think carefully about how validator set transitions happen and how one validator set "passes the baton" to the next.
+The above assumes that there is a single set of validators that never changes. In reality, however, we want validators to be able to join and leave. This introduces two classes of considerations. First, all of the above math assumes that the validator set that prepares and commits any two given checkpoints is identical. If this is not the case, then there may be situations where two conflicting checkpoints get finalized, but no one can be slashed because they were finalized by two completely different validator sets. 
 
-<copy text here>
+![](https://cdn-images-1.medium.com/max/800/1*3YfbZO5xwAxt-DrUIo2CmA.jpeg)
 
-Second, we need to establish what is the specific mechanism by which validators can join and leave. We start off with a simple one: validators apply to join the validator set by sending a transaction containing (i) the ETH they want to deposit, (ii) the "validation code" (a kind of generalized public key), and (iii) the return address that their deposit will be sent to when they withdraw. If this transaction gets included during dynasty N, then they become part of dynasty N + 2, as well as all future dynasties until they decide to log off. The two-dynasty delay ensures that the joining transaction will be confirmed by the time dynasty N + 1 begins, and so any candidate blocks that initiates dynasty N + 2 is guaranteed to have the same validator set for dynasty N + 2. Leaving the validator set is symmetrical: validators can send a transcation to log off in dynasty N, which takes effect in dynasty N + 2.
+Hence, we need to think carefully about how validator set transitions happen and how one validator set "passes the baton" to the next. One nautral possibility is to only change the validator set if an epoch was finalized. This resolves the problem in its simplest form, as it means that there is no way to skip to the next validator set without finalizing a block with the previous validator set first.
+
+However, this is still not a complete solution because it fails to take into account that the fact of whether or not an epoch was finalized _is itself something we do not yet have consensus on_. Hence, there exists a possible failure mode where two children get made on top of the same parent, where from one child's view the parent was finalized and from the other child's view the parent was not finalized:
+
+![](https://cdn-images-1.medium.com/max/800/1*LZg61-hOWkuYH1pcgO3gYQ.png)
+
+There are three ways out. One is for nodes to wait for two rounds of "finality" before considering a block finalized; one cannot achieve finality for both children without the signatures of the second round on one side and the first round of the other side intersecting. A second is to limit the rate at which validators can be swapped in and out, ensuring fault tolerance still stays close to 1/3. A third is to require signatures from both 2/3 of the current validator set and 2/3 of the previous validator set in order to consider a set of prepares or commits sufficient.
+
+![](https://cdn-images-1.medium.com/max/800/1*RlTtXf7ymF-qyBwmtAb3GA.jpeg)
+
+![](https://cdn-images-1.medium.com/max/800/1*O1Tj6HvCiavDdHPVGrLJKg.png)
+
+We make one modification to the fork choice rule: instead of taking the descendant with the highest percentage of commits from "the" validator set, we take the descendant checkpoint where the _minimum_ of (i) the percentage of that checkpoint's _current_ validator set that committed, and (ii) the percentage of that checkpoint's _previous_ validator set that committed, is maximized.
+
+### Joining and Leaving
+
+Now, we need to establish what is the specific mechanism by which validators can join and leave. We start off with a simple one:
+
+* Validators apply to join the validator set by sending a transaction containing (i) the ETH they want to deposit, (ii) the "validation code" (a kind of generalized public key), and (iii) the return address that their deposit will be sent to when they withdraw.
+* If this transaction gets included during dynasty N, then they become part of dynasty N + 2, as well as all future dynasties until they decide to log off.
+* Validators can "log off" by sending a transaction to do so. If it is included during dynasty N, then they will be logged off starting from dynasty N + 2.
+* If a validator has been logged off for the past consecutive four months, then the validator can send another transaction to withdraw their deposit to their return address.
+
+The two-dynasty delay ensures that the joining transaction will be confirmed by the time dynasty N + 1 begins, and so any candidate blocks that initiates dynasty N + 2 is guaranteed to have the same validator set for dynasty N + 2.
+
+Note that the possibility of validator sets changing, and validators withdrawing their deposits, opens up another risk: **long-range attacks**. If a client has been logged off for more than four months, then there is a risk that a malicious majority of former validators, who were active at the time the client was now online but are now no longer active, can finalize a chain conflicting with the main chain, send this chain to the client, and the client will accept it. This necessarily means that at least half of this malicious majority violated a slashing condition, and under normal circumstances it would mean that their deposits are fully lost. In this case, however, _the offending validators have already taken their money out_; hence, they cannot be penalized.
+
+This problem is not fully resolvable, unless we are willing to adopt a system where validators can never recover their deposits. What we _can_ do, however, is better understand the precise requirements that we are imposing on clients and the network. A message should be considered "cryptoeconomically meaningful" only if the message is signed by a validator whose deposit is still certainly in the main chain. The way we can test this is that the client can keep track of the time that they most recently received a each finalized checkpoint, and only accept a child checkpoint if this checkpoint is received less than four months after the predecessor. This implies that in order to remain synchronized with the chain, clients need to be logged on every four months, and assuming clients are online constantly it implies a network synchrony assumption: any message signed can reach any node within two months (half of four months, as if a client detects a validator violating a slashing condition, the message needs to be included into a block before that validator can withdraw in order to destroy theire deposit).
 
 ### Economic Fundamentals
 
-The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.
+The fault-tolerance-theoretic assumptions made so far simply assume that more than two thirds of every validator set is not willing to lose theire entire deposits, and given this assumption we can show safety. However, we must also show how the algorithm incentivizes liveness, and so so under several different sets of assumptions. We analyze the proof of stake component under both an uncoordinated choice model and a coordinated choice model. For now we assume that the underlying proof of work blockchain simply works, and ask our readers to accept this in light of uncoordinated choice modeling [cite http://nakamotoinstitute.org/static/docs/anonymous-byzantine-consensus.pdf] and empirical observations that coordinated attacks on proof of work have been rare so far, though in a later section we will discuss how validators can cooperate to overcome 51% attacks against the underlying proof of work layer.
 
 ### Protocol utility function
  
@@ -133,7 +160,9 @@ Where:
 
 Note that there is no single principled way to say what the protocol utility is; this is a question that ultimately rests on the values of the users of the system. However, we can defend the reasoning behind each component in the above formula.
 
-The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait `k` epochs for their transaction to be finalized is logarithmic in `k`. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. Another approach is to look at the possible set of blockchain applications, ranging from running games on them at the 100-1000 millisecond level, to retail payments at the 1-10 second level, other kinds of payments that currently take 1-10 minutes, and large institutional settlements that can take days, and see that they are roughly logarithmically distributed on the scale of the longest confirmation time that they could reasonably accept. The separate `c` term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.
+The -M * SF term is self-explanatory; safety failures are very bad, as it means that events that appear to have been finalized, and that users may be relying on being finalized, suddenly become unfinalized. The -ln(i - LFE(i)) term is more complicated. What is it saying is that the amount of pain that users feel from having to wait `k` epochs for their transaction to be finalized is logarithmic in `k`. This can be justified inuitively: the difference between finality in 1 minute and 2 minutes feels similar in size to the difference between 1 hour and 2 hours. The separate `c` term is there to show that even if a given epoch does not finalize, commits can still provide value, as a smaller number of commits on a given block can still make it harder to finalize competing blocks.
+
+The purpose of this function is to motivate the incentive structure, and show how large losses in protocol utility lead to proportionately large penalties for the perpetrator.
 
 ### Incentives
 
@@ -166,6 +195,7 @@ We define the penalties as follows:
 * All non-preparing validators pay `NPP`
 * Suppose `cp` is the minimal fraction of validators between the two validator sets that commits (eg. if 80% of the validators in the current dynasty commit and 68% of the validators in the previous dynasty do, `cp = 0.68`). All validators pay `NCCP * (1 - cp)`. Waived if 2/3 prepares are not found (ie. validators cannot legally commit).
 * Suppose `pp` is the minimal fraction of validators between the two validator sets that prepares. All validators pay `NPCP * (1-pp)`
+* If a validator violates a slashing condition, they lose their entire deposit.
 
 #### Uncoordinated Choice
 
@@ -287,17 +317,22 @@ There are other solutions; for example, (3, 3, 3, 3, 1) is interesting because i
 
 Suppose that there exists a coalition of size >= 1/3 (possibly even size >= 2/3) that engages in attacks of type (5), (6) or (7) above. This type of attack can be resolved in honest nodes' favor, but in many cases (especially those where the dishonest coalition is of size >= 1/2) this requires some out-of-band coordination between users, which can only partially be automated. This does require a synchrony assumption between validators and users, but one on the order of weeks (more precisely, the synchrony assumption must be on the same order as the amount of time that a >33% attack will take to resolve; resolution taking weeks is arguably acceptable because the prepetrators will lose a large portion of their deposits in this kind of attack).
 
-Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the second.
+Such an attack and resolution would proceed as follows. First, suppose that a validator with >= 1/3 of nodes simply stops committing, or logs out outright and stops committing and preparing. The two cases are alike so we can consider just the first.
 
-The offline validator loses `(NCP + NPP + NPCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. Online validators lose `(NCP + NPCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. With the "griefing factor bound 2" settings, this gives a loss of 1.5 + 3.75 + 1.25 + 1 = 7.5 for the offline validator and a loss of 1.5 + 1.25 + 1 = 3.75 for online validators, so the offline validator's balance drains twice as quickly. Suppose that the original fraction of the offline validator is p > 1/3, and let t be the fraction of each online validator's balance remaining. Users need to wait until the balances decrease, to the point where `p * t**2 = 1/2 * (1 - p) * t`, or `t = (1-p) / 2p`. For example, if 40% of validators drop offline, then `t = 0.75`, and so online validators will lose 25% of their funds and offline validators will lose 43.75%.
+The offline validator loses `(NCP + NCCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. Online validators lose `(NCCP * 1/3 + NFP) * PENALTY_FACTOR` times their balance. With the "griefing factor bound 2" settings of (1, 1, 1, 1, 0), this gives a loss (expressed as percentage of total deposit) of 1 + 1/3 for the offline validator and a loss of 1/3 for online validators, so the offline validator's balance drains four times as quickly. If the online validator's share is 40% (ie. offline validator has 0.4x, online validators have 0.6x), for example, then the blockchain will once again commit when the balances decrease to (offline 0.272, online 0.545), at which point online validators once again have more than two thirds.
 
-Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future, where `t = 1/2` (say, this is after three weeks). It's entirely possible for two thirds of the validator set in C1 to finalize C1, where the remaining one third is precisely the two thirds of the validator set in C2 that then finalizes C2.
+Note that this real-time reduction of deposits does introduce a new consideration: if there are two conflicting checkpoints that finalize, the validator sets between the two checkpoints can now differ. In the most extreme case, this implies the possibility of two conflicting finalizing checkpoints where on one of the two checkpoints no deposits are lost. For example, consider the case of two finalized checkpoints C1 and C2, where C1 comes one epoch after the previous finalized checkpoint, but C2 comes long in the future. Suppose that the validator set is split into groups A and B, where A finalizes C1 and B finalizes C2. At the time of C1, the size of A is 0.667x, and the size of B is 0.333x. At the time of C2, the size of A is reduced to 0.111x, and the size of B is reduced to 0.222x. Hence, A can finalize C1 and B can finalize C2 with no slashing conditions violated.
 
-[diagram]
+![](http://vitalik.ca/files/CommitsSync.png)
 
-This can be resolved with a synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).
+The purpose of this attack would be to convince a node that has been offline between C1 and C2 that C2 is the correct chain, when in reality it is C1 that is the correct chain. B would lose a large portion of their deposits on the C2 chain, but the C2 chain has little economic value as it is only used for this one particular attempt to defraud a set of clients, and so the attacker would emerge unscathed on the C1 chain.
 
-More formally, if C2 comes after C1, and the t values are t(C2) and t(C1), then the amount of equivocation required is `(2/3 * t(C2) + 2/3 * t(C1)) - t(C1)`, and inside of C1 `1 - t(C1)` would be lost due to the non-validation penalties - a total loss of `2/3 * t(C2) - 1/3 * t(C1) + 1 - t(C1)`, or `2/3 * t(C2) + 1 - 4/3 * t(C1)`. Regardless of `t(C2)`, this is clearly minimized when `t(C1) = 1`, so we have `2/3 * t(C2) - 1/3`. With the above synchrony assumption, we only need to be concerned about C2 if the distance is C1 and C2 is sufficiently small, and so we can specify a lower bound on `t(C2)`.
+This can be resolved by strengthening the synchrony assumption. If the node is constantly online, then it should refuse to accept C2 until three weeks have actually passed, and so as long as C1 can reach the node within three weeks there is no security risk (more precisely, latencies that are significant but below three weeks can reduce the amount of equivocation needed for double finalization, perhaps from 1/3 to 32.5% if latency is a day or 25% if latency is a week, though the exact figures depend on the exact formula used).
+
+Here are the results for the formulas above; note that the delay until finality can easily be scaled proportionately by any value.
+
+![](http://vitalik.ca/files/diag1.png)
+![](http://vitalik.ca/files/diag2.png)
 
 Now, let us consider the attacks where the censoring coalition is >= 1/2. Then, minority validators will refuse to build on chains that are censoring them, and so they will coordinate on their own chain. The result will be exactly the same as the result above: a majority chain and a minority chain, where under the rules of the protocol the majority chain will be able to finalize first, and where on the majority chain the victims will lose money faster than the attackers and so the attackers will be even stronger.
 

casper4/griefing_one_third_offline_simulator.py

@@ -16,16 +16,20 @@ def sim_offline(p):
     online, offline = 1-p, p
     for i in range(1, 999999):
         # Lost by offline validators
-        offline_loss = NFP + NPP + NPCP * offline
+        offline_loss = NFP + NPP + NPCP * (offline / (online + offline))
         # Lost by online validators
-        online_loss = NFP + NPCP * offline
+        online_loss = NFP + NPCP * (offline / (online + offline))
         online *= 1 - increment * math.log(i) * online_loss
         offline *= 1 - increment * math.log(i) * offline_loss
         if i % 100 == 0 or online >= 2 * offline:
-            print("%d epochs (%.2f days): online %.3f offline %.3f" %
+            print("%d epochs (%.2f days): online %.4f offline %.4f" %
                   (i, epoch_len * i / 86400, online, offline))
             # If the remaining validators can commit, break
             if online >= 2 * offline:
-                break
+                return (1-p, online, epoch_len * i / 86400)
 
 sim_offline(0.4)
+
+#results = [sim_offline(i * 0.01) for i in range(34, 100)]
+#for col in results:
+#    print("%.4f, %.4f, %.4f" % col)